题目内容
6.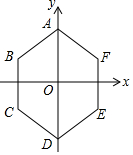 如图,正六边形ABCDEF中,顶点A,D的坐标分别是(0,1)和(0,-1),求点B,E的坐标.
如图,正六边形ABCDEF中,顶点A,D的坐标分别是(0,1)和(0,-1),求点B,E的坐标.
分析 直接利用正六边形的性质得出△ABO是等边三角形,且AB=BO=AO=1,进而得出答案.
解答  解:如图所示:连接BO,
解:如图所示:连接BO,
∵正六边形ABCDEF中,顶点A,D的坐标分别是(0,1)和(0,-1),
∴△ABO是等边三角形,且AB=BO=AO=1,
∴BN=$\frac{1}{2}$,则NO=$\frac{\sqrt{3}}{2}$,
故B点坐标为:(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),可得B,E点关于原点对称,
则E点坐标为:($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
点评 此题主要考查了正多边形和圆,正确掌握正六边形的性质是解题关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
11.下列一元二次方程没有实数解的是( )
| A. | x2-3x=0 | B. | x2=x-3 | C. | x2-3=0 | D. | (x-1)(x-2)=0 |
15.不使用计算器,你能估算出126的算术平方根的大小应在哪两个整数之间吗?( )
| A. | 10~11之间 | B. | 11~12之间 | C. | 12~13之间 | D. | 13~14之间 |
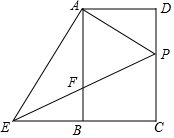 如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.
如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.