题目内容
1.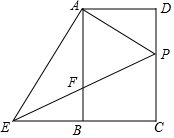 如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.
如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.(1)求证:△ADP∽△ABE;
(2)若AD:AB=2:3,且CP=2DP,求AF:FB的值.
分析 (1)根据两角对应相等两三角形相似即可证明.
(2)延长AD、EP交于点M.设AD=4a,CD=6a,则PC=4a,DP=2a,想办法求出AM、EB,由AM∥EB,得$\frac{AF}{FB}$=$\frac{AM}{EB}$,由此即可解决问题.
解答 (1)证明: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠ABC=∠BAD=∠ADC=∠ABE=90°,
∵∠EAP=∠BAD=90°,
∴∠EAB=∠PAD,∵∠ABE=∠ADP,
∴△ADP∽△ABE.
(2)解:如图,延长AD、EP交于点M.
∵AD:AB=2:3,且CP=2DP,
∴可以假设AD=4a,CD=6a,则PC=4a,DP=2a,
∵△ADP∽△ABE,
∴$\frac{AD}{AB}$=$\frac{DP}{EB}$,
∴$\frac{4a}{6a}$=$\frac{2a}{EB}$,
∴EB=3a,
∵DM∥EC,
∴$\frac{DM}{EC}$=$\frac{DP}{PC}$,
∴$\frac{DM}{7a}$=$\frac{2a}{4a}$,
∴DM=$\frac{7}{2}$a,AM=$\frac{15}{2}$a,
∵AM∥EB,
∴$\frac{AF}{FB}$=$\frac{AM}{EB}$=$\frac{\frac{15}{2}a}{3a}$=$\frac{5}{2}$.
点评 本题考查矩形的性质.相似三角形的判定和性质、平行线分线段成比例定理等 知识,解题的关键是学会利用参数解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.观察下列各式数:-2x,4x2,-8x3,16x4,-32x5,…则第n个式子是( )
| A. | -2n-1xn | B. | (-2)n-1xn | C. | -2nxn | D. | (-2)nxn |
13.在-8,2.6,-3$\frac{1}{2}$,0,2$\frac{2}{3}$,-5.7中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
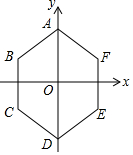 如图,正六边形ABCDEF中,顶点A,D的坐标分别是(0,1)和(0,-1),求点B,E的坐标.
如图,正六边形ABCDEF中,顶点A,D的坐标分别是(0,1)和(0,-1),求点B,E的坐标.