题目内容
14．约分：（1）-$\frac{12{a}^{2}b}{3ab}$
（2）$\frac{3（a-b）}{12（a-b）^{2}}$
（3）$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$．
分析 将分子与分母约去公因式即可；
解答 解：（1）-$\frac{12{a}^{2}b}{3ab}$=-4a
（2）$\frac{3（a-b）}{12（a-b）^{2}}$=$\frac{1}{4（a-b）}$
（3）$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$=$\frac{x+1}{x-1}$
点评 此题主要考查了约分，正确分解因式是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
19．$\sqrt{x}$+$\sqrt{y}$的一个有理化因式是（ ）
| A． | $\sqrt{x+y}$ | B． | $\sqrt{x}-\sqrt{y}$ | C． | $\sqrt{x}+\sqrt{y}$ | D． | $\sqrt{x-y}$ |
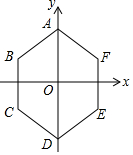如图，正六边形ABCDEF中，顶点A，D的坐标分别是（0，1）和（0，-1），求点B，E的坐标．
3．下列各组数相等的是（ ）
| A． | -32与（-3）2 | B． | -33与（-3）3 | C． | -|-1|与-（-1） | D． | 23与32 |