题目内容
15．先阅读下面的材料，再解答问题：已知1+x+x2+x3+x4+x5=0，求x6的值
解：∵1+x+x2+x3+x4+x5=0
∴x6=1+x+x2+x3+x4+x5+x6
=1+x（1+x+x2+x3+x4+x5）
=1+0=1
根据以上材料求下面问题：已知x2+x=-1，求x2013+x2012+x2011+…x3+x2+x的值．
分析 首先分组分解代数式x+x2+x3+…+x2013，整体代入得出代数式结果．
解答 解：∵1+x+x2=0，
∴x+x2+x3+…+x2013
=x（1+x+x2）+x3（1+x+x2）+…+x2011（1+x+x2）
=0．
点评 此题考查因式分解的运用，分组分解和整体代入是解决问题的关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
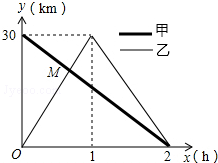在一条笔直的公路上有A，B两地，甲骑自行车从A地到B地，乙骑摩托车从B地到A地，到达A地后立即按原路返回，下图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：