题目内容
18.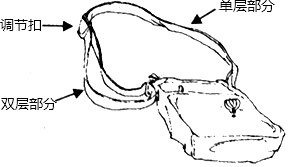 如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:| 单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
| 双层部分的长度y(cm) | … | 73 | 72 | 71 | … |
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
分析 (1)观察表格可知,y是x的一次函数,设y=kx+b,利用待定系数法即可解决问题;
(2)列出方程组即可解决问题;
(3)由题意当y=0,x=150,当x=0时,y=75,可得75≤l≤150.
解答 解:(1)观察表格可知,y是x的一次函数,设y=kx+b,
则有$\left\{\begin{array}{l}{4k+b=73}\\{6k+b=72}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=75}\end{array}\right.$,
∴y=-$\frac{1}{2}$x+75.
(2)由题意$\left\{\begin{array}{l}{x+y=120}\\{y=-\frac{1}{2}x+75}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=90}\\{y=30}\end{array}\right.$,
∴单层部分的长度为90cm.
(3)由题意当y=0,x=150,当x=0时,y=75,
∴75≤l≤150.
点评 本题考查一次函数的应用、待定系数法等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
9.用计算器计算时,下列说法错误的是( )
| A. | 计算“$\frac{1}{2}$-1$\frac{3}{4}$”的按键顺序是 | |
| B. | 计算“3×105-28”的按键顺序是 | |
| C. | “已知SinA=0.3,求锐角A”的按键顺序是 | |
| D. | 计算“($\frac{1}{2}$)5”的按键顺序是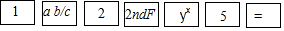 |
13.中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第六天走的路程为( )
| A. | 24里 | B. | 12里 | C. | 6里 | D. | 3里 |
3. 阅读下列材料:
阅读下列材料:
实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
下面是小明的探究过程,请补充完整:
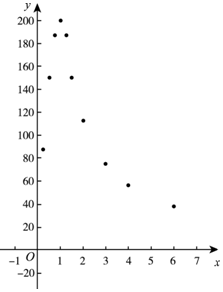
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=$\frac{3}{2}$两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.
 阅读下列材料:
阅读下列材料:实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小明根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
| 饮酒后的时间x (小时) | … | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ | 1 | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | 6 | … |
| 血液中酒精含量y (毫克/百毫升) | … | $\frac{175}{2}$ | 150 | $\frac{375}{2}$ | 200 | $\frac{375}{2}$ | 150 | $\frac{225}{2}$ | $\frac{225}{3}$ | $\frac{225}{4}$ | 45 | $\frac{225}{6}$ | … |
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线x=$\frac{3}{2}$两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上6:30能否驾车去上班?请说明理由.
7.$\frac{\stackrel{m个2}{\overbrace{2×2×…×2}}}{\underset{\underbrace{3+3+…+3}}{n个3}}$=( )
| A. | $\frac{2m}{{3}^{n}}$ | B. | $\frac{{2}^{m}}{3n}$ | C. | $\frac{2m}{{n}^{3}}$ | D. | $\frac{{m}^{2}}{3n}$ |
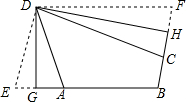 定义:有三个内角相等的四边形叫三等角四边形.
定义:有三个内角相等的四边形叫三等角四边形.
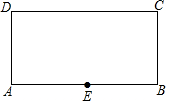 如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.
如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.


