题目内容
13.中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第六天走的路程为( )| A. | 24里 | B. | 12里 | C. | 6里 | D. | 3里 |
分析 设第一天走了x里,则第二天走了$\frac{1}{2}$x里,第三天走了$\frac{1}{2}$×$\frac{1}{2}$x…第六天走了($\frac{1}{2}$)5x里,根据路程为378里列出方程并解答.
解答 解:设第一天走了x里,
依题意得:x+$\frac{1}{2}$x+$\frac{1}{4}$x+$\frac{1}{8}$x+$\frac{1}{16}$x+$\frac{1}{32}$x=378,
解得x=192.
则($\frac{1}{2}$)5x=($\frac{1}{2}$)5×192=6(里).
故选:C.
点评 本题考查了一元一次方程的应用.根据题意得到($\frac{1}{2}$)5x里是解题的难点.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
4.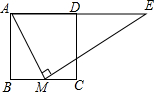 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )| A. | 18 | B. | $\frac{109}{5}$ | C. | $\frac{96}{5}$ | D. | $\frac{25}{3}$ |
18.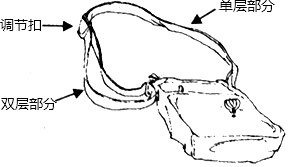 如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
(1)根据表中数据的规律,完成以下表格,并直接写出y关于x的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
 如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:| 单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
| 双层部分的长度y(cm) | … | 73 | 72 | 71 | … |
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
5.有这样一个问题:探究函数y=x-1+$\frac{1}{x-2}$的图象与性质.
下面是小东的探究过程,请补充完成:
(1)函数y=x-1+$\frac{1}{x-2}$的自变量x的取值范围是x≠2.
(2)在平面直角坐标系xOy中描出了图象上的一些点,请你画出函数的图象;
下表是y与x的几组对应值.
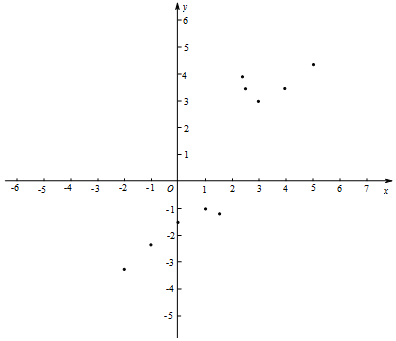
(3)求m的值;
(4)根据图象写出此函数的一条性质.
下面是小东的探究过程,请补充完成:
(1)函数y=x-1+$\frac{1}{x-2}$的自变量x的取值范围是x≠2.
(2)在平面直角坐标系xOy中描出了图象上的一些点,请你画出函数的图象;
下表是y与x的几组对应值.
| x | … | -2 | -1 | 0 | 1 | 1.4 | 2.4 | 2.5 | 3 | 4 | 5 | … |
| y | … | -3.25 | -2.33 | -1.50 | -1 | -1.27 | 3.9 | 3.5 | 3 | m | 4.33 | … |

(3)求m的值;
(4)根据图象写出此函数的一条性质.
2.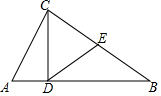 如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )
如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )
 如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )
如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )| A. | 60° | B. | 75° | C. | 90° | D. | 105° |
3.已知某种细菌的直径为0.0000302mm,用科学记数法表示为( )
| A. | 3.02×10-5mm | B. | 30.2×10-6mm | C. | 302×10-4mm | D. | 302×10-8mm |
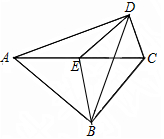 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为32度.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为32度.