题目内容
5.某商店以一定的价格购进某种干果若干千克,对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,于不同时间销售完;甲级干果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=-x2+40x;乙级干果从开始销售至销售的第x天的总销量y2(千克)与x的关系为是二次函数,且乙级干果的前三天的销售量的情况见表:| x | 1 | 2 | 3 |
| y2 | 58 | 112 | 162 |
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
分析 (1)根据题意列方程组即可得到结果;
(2)根据题意解方程即可得到结论;
(3)设两种干果的总销量的差为z,根据题意得到z=-2x2+60x-(-x2+40x)=-x2+20x,然后求二次函数的最大值即可.
解答 解:(1)设y2=ax2+bx+c,
把(1,58)(2,112)(3,162)代入上式得$\left\{\begin{array}{l}{a+b+c=58}\\{4a+2b+c=112}\\{9a+3b+c=162}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=60}\\{c=0}\end{array}\right.$.
故乙级干果第x天的总销量y2(千克)与x的函数关系式为:y2=-2x2+60x;
(2)甲级干果y=-x2+40x=-(x-20)2+400,当x=20时,甲级干果卖完,
乙级干果y=-2x2+60x=-2(x-15)2+450,当x=15时,乙级干果卖完,
∴当一种干果销售完5天后,另一种干果才销售完;
(3)设两种干果的总销量的差为z,
则z=-2x2+60x-(-x2+40x)=-x2+20x=-(x-10)2+100,
∴当x=10时,z最大=100,
∴销售第10天时,两种干果的总销量相差最大.
点评 本题考查了二次函数的应用,待定系数法求二次函数的解析式,关键是根据表格代入数列出三元一次方程组求出a和b,c,确定函数式,然后根据等量关系和列方程求解.

练习册系列答案
相关题目
16.与方程x+1=0的解相同的方程是( )
| A. | 2x+3=0 | B. | 4x=5x-2 | C. | 2(x+1)=0 | D. | 3x+3-2x=0 |
13.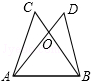 如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
 如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
如图,AD=BC,AC=BD,则下列结论中,不正确的是( )| A. | OA=OB | B. | OC=OD | C. | ∠C=∠D | D. | ∠OAB=∠DBA |
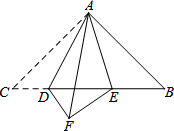 已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
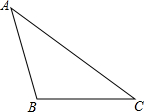 如图,已知△ABC,请按下列要求作图:
如图,已知△ABC,请按下列要求作图: