题目内容
20.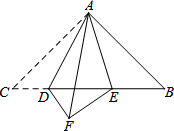 已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.(1)求证:△AEF≌△AEB;
(2)∠DFE=90°.
分析 (1)根据折叠的性质得到△AFD≌△ADC,根据全等三角形的性质得到AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD,由于AB=AC,于是得到AF=AB,证得∠FAE=∠BAE,即可得到结论;
(2)由(1)知△AFE≌△ABE,根据全等三角形的性质得到∠AFE=∠C,EF=EC,即可得到结论.
解答 解:(1)∵把△ADC沿着AD折叠,得到△ADF,
∴△AFD≌△ADC;
∴AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD,
∵AB=AC,
∴AF=AB,
∵∠DAE=45°,
∴∠FAE=∠BAE,
在△AFE与△ACE中,
$\left\{\begin{array}{l}{AF=AB}\\{∠FAE=∠BAE}\\{AE=AE}\end{array}\right.$,
∴△AFE≌△ABE,
(2)由(1)知△AFE≌△ABE,
∴∠AFE=∠C,EF=EC,
∴∠DFE=∠DFA+∠EFA=∠B+∠C=90°.
故答案为:90°.
点评 本题考查了全等三角形的判定和性质,轴对称的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
12.如果式子m-7与4m-9互为相反数,则m的值为( )
| A. | $\frac{16}{3}$ | B. | -$\frac{16}{3}$ | C. | $\frac{16}{5}$ | D. | -$\frac{16}{5}$ |
5.某商店以一定的价格购进某种干果若干千克,对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,于不同时间销售完;甲级干果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=-x2+40x;乙级干果从开始销售至销售的第x天的总销量y2(千克)与x的关系为是二次函数,且乙级干果的前三天的销售量的情况见表:
(1)求乙级干果滴x天的总销量y2(千克)与x的函数关系式(不需要写自变量的取值范围);
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
| x | 1 | 2 | 3 |
| y2 | 58 | 112 | 162 |
(2)求:当一种干果销售完多长时间后,另一种干果才销售完?
(3)销售第几天时,两种干果的总销量相差最大?
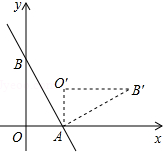 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.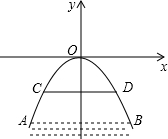 如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?
如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?