题目内容

15．计算
①（-3x2y4z）÷9x4y5•x5（x2y）2
②（x-3）2+3x-9
③（x-$\frac{1}{4}$）（3x+$\frac{3}{4}$）
④用乘法公式计算：102×98．

分析 ①原式先计算乘方运算，再计算乘除运算即可得到结果；
②原式利用完全平方公式化简，合并即可得到结果；
③原式利用多项式乘以多项式法则计算即可得到结果；
④原式变形后，利用平方差公式计算即可得到结果．

解答 解：①原式=①（-3x2y4z）÷9x4y5•x5•x4y2=-$\frac{1}{3}$x7y3z；
②原式=x2-6x+9+3x-9=x2-3x；
③原式=3x2+$\frac{3}{4}$x-$\frac{3}{4}$x-$\frac{3}{16}$=3x2-$\frac{3}{16}$；
④原式=（100+2）×（100-2）=10000-4=9996．

点评 此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
5．某商店以一定的价格购进某种干果若干千克，对其进行筛选分成甲级干果与乙级干果后同时开始销售．这批干果销售结束后，店主从销售统计中发出：甲级干果与乙级干果在销售过程中每天都有销量，于不同时间销售完；甲级干果从开始销售至销售的第x天的总销量y1（千克）与x的关系为y1=-x2+40x；乙级干果从开始销售至销售的第x天的总销量y2（千克）与x的关系为是二次函数，且乙级干果的前三天的销售量的情况见表：
x123
y258112162
（1）求乙级干果滴x天的总销量y2（千克）与x的函数关系式（不需要写自变量的取值范围）；
（2）求：当一种干果销售完多长时间后，另一种干果才销售完？
（3）销售第几天时，两种干果的总销量相差最大？
6．某经销商销售的猕猴桃的进价是每千克5.7元，销售中约有5%的正常损耗．当销售价定为每千克9元时，每天可销售100千克，商家想采用提高销量的办法来增加利润，经试销发现：这种猕猴桃每千克的销售价每提高0.10元每天的销售量就下降10千克，且平均每天的其他成本为50元．
（1）商家把猕猴桃的销售价至少定为每千克多少元时，才能避免亏本？
（2）求猕猴桃每天的销售量y（千克）与售价x（元/千克）之间的函数关系式．
（3）当猕猴桃销售价定为多少元时，才能使商家一天的利润最大？一天的最大利润时多少元？
3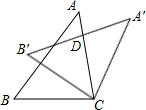．如图，把△ABC绕点C顺时针旋转32°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A度数为（　　）
A．48°B．58°C．68°D．78°
10．用如图所示的三种不同花色的地砖铺成如图b的地面图案．
（1）如果用①+②+③+④+⑤+⑥+⑦+⑧+⑨的方法计算地面面积，请列出整式并化简；
（2）你有更简便的算法吗？请你列出式子；
（3）你认为由（1）（2）两种方法得到的两个式子有什么关系？为什么？
20．已知点C（b，d），D（c，d），且d≠0，b≠c，那么直线CD与坐标轴有什么位置关系？
7．数学课上，李老师出示了如下题目：在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图所示，试确定线段AE与DB的大小关系，并说明理由．

小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点E为AB中点时，如图①，请你确定AE与DB的大小关系，并说明理由．
（2）特例启发，解决问题
当点E是AB上任一点时，AE与DB的大小关系是：AE=DB．
理由如下：如图②，过点E作EF∥BC，交AC于点F．（请你完成解答过程）
（3）拓展结论，设计新题
已知等边三角形ABC的边长为1，AE=2，且ED=EC．（请你直接写出下列结果）
①若点E在边AB的延长线上，点D在边CB的延长线上，则CD=3
②若点E在边BA的延长线上，点D在边BC的延长线上，则CD=1．
4．某工作人员打算利用铝合金材料制成一个面积为6m2的直角三角形模具，设直角三角形模具的一条直角边长为xm，另一条直角边长为ym．
（1）写出y与x之间的函数关系式，并说明y与x之间是什么函数关系；
（2）若使模具的一条直角边比另一条直角边多1m．已知每米这种铝合金材料的价格为5元，制作这个模具共花多少钱？
5．方程x2-4x+4=0的根是（　　）
A．x=2B．x1=x2=2C．x=4D．x1=x2=4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网