题目内容
2. 如图是二次函数y=ax2+bx+c的部分图象,在下列四个结论中正确的是①③(写出所有正确结论的序号)
如图是二次函数y=ax2+bx+c的部分图象,在下列四个结论中正确的是①③(写出所有正确结论的序号)①不等式ax2+bx+c>0的解集是-1<x<5;
②a-b+c>0;
③b2-4ac>0;
④4a+b<0.
分析 根据图象可得抛物线与x轴的另一个交点为(-1,0),当y>0时,-1<x<5,故①正确;当x=-1时,y=a-b+c=0,故②错误;根据与x轴的交点坐标判断出③正确;抛物线对称轴为直线x=2,判断出④错误.
解答 解:∵图象可得抛物线与x轴的另一个交点为(-1,0),
∴当y>0时,-1<x<5,故①正确;
当x=-1时,y=a-b+c=0,故②错误;
∵抛物线与x轴的交点有两个,∴b2-4ac>0,故③正确;
∵抛物线的对称轴为直线x=2,∴-$\frac{b}{2a}$=2,4a+b=0,故④错误.
故答案为①③.
点评 本题考查了二次函数图象与系数的关系,系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点确定,掌握二次函数的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.为鼓励民众节约用电,城镇居民生活用电电费目前实行梯度收费,具体标准如下表:
(1)若月用电100千瓦时,应交电费多少元?若月用电200千瓦时,应交电费多少元?
(2)若某用户12月应交电费93元,该用户12月的用电量是多少?
| 月用电量(单位:千瓦时) | 单价(单位:元) |
| 150以内(含150) | 0.5 |
| 超过150但不超过300的部分(含300) | 0.6 |
| 300以上(不含300)的部分 | 0.8 |
(2)若某用户12月应交电费93元,该用户12月的用电量是多少?
7.化简(x-1-1)-1的结果是( )
| A. | $\frac{x}{1-x}$ | B. | $\frac{x}{x-1}$ | C. | x-1 | D. | 1-x |
12.某工艺品生产厂为了按时完成订单,对员工采取生产奖励活动,奖励办法以下表计算奖励金额,但是一个月后还是不能按时完成,厂家请工程师改进工艺流程,提高了产量.改进工艺前一月生产A、B两种工艺品共413件,改进工艺后的第一个月生产这两种工艺品共510件,其中A和B的生产量分别比改进工艺前一个月增长25%和20%.
(1)在工艺改进前一个月,员工共获得奖励金额多少元?
(2)如果某车间员工想获得5500元奖金,需要生产多少件工艺品;
(3)改进工艺前一个月,生产的A、B两种工艺品分别为多少件?
| 产量(x件) | 每件奖励金额(元) |
| 0<x≤100 | 10 |
| 100<x≤300 | 20 |
| x>300 | 30 |
(2)如果某车间员工想获得5500元奖金,需要生产多少件工艺品;
(3)改进工艺前一个月,生产的A、B两种工艺品分别为多少件?
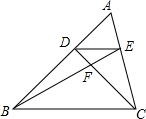 如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$.
如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$. 如图所示,数轴的单位长度为1.
如图所示,数轴的单位长度为1.