题目内容
9.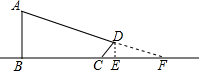 小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.
小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.
分析 先根据CD的长以及坡角求出落在斜坡上的影长在地面上的实际长度,即可知AB的总影长,然后根据1 m杆的影子长为2 m,求解电线杆的高度.
解答  解:作DE⊥BC交BC延长线于E,作DF⊥AB于F,
解:作DE⊥BC交BC延长线于E,作DF⊥AB于F,
由题意可知:∠DCE=45°,
∵CD=2m,
∴DE=CE=$\sqrt{2}$m,
∴DF=BE=BC+CE=(10+$\sqrt{2}$)m,
又∵某一时刻测得1m的杆子在阳光下的影子长为2m,
∴$\frac{AF}{DF}$=$\frac{1}{2}$,
∴AF=$\frac{10+\sqrt{2}}{2}$,
∵四边形BFDE为矩形,
∴DE=BF=$\sqrt{2}$m,
∴电线杆的高度AB=AF+BF=$\frac{10+\sqrt{2}}{2}$+$\sqrt{2}$=$\frac{10+3\sqrt{2}}{2}$m.
点评 考查了相似三角形的应用,注意;影子平行于物体时,影子和物体的实际高度相等;影子垂直于物体时,根据:同一时刻物高与影长成比例进行计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知一元二次方程x2-2x-1=0的两根分别为x1,x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值为( )
| A. | 2 | B. | -1 | C. | $-\frac{1}{2}$ | D. | -2 |
 2016年1月21日01:13:13,青海海北州门源县发生6.4级地震.接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
2016年1月21日01:13:13,青海海北州门源县发生6.4级地震.接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: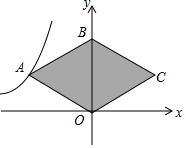 如图,O是坐标原点,菱形OABC的顶点B的坐标为(0,4),反比例函数y=-$\frac{8}{x}$(x<0)的图象经过点A,则菱形OABC的面积为16.
如图,O是坐标原点,菱形OABC的顶点B的坐标为(0,4),反比例函数y=-$\frac{8}{x}$(x<0)的图象经过点A,则菱形OABC的面积为16.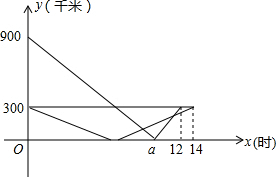 甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留2小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:
甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留2小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题: