题目内容
3.如图1,已知点A,B是反比例函数y=$\frac{k}{x}$(k>0)图象上的任意两点,过点A,B作直线交y轴于点C,交x轴于点D.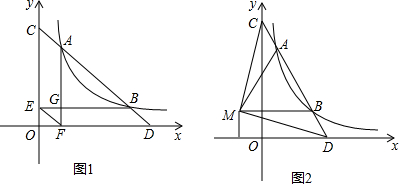
(1)过点A作AF⊥x轴于点F,过点B作BE⊥y轴于点E,连接EF,请说明:①EF∥AB;②AC=BD;
(2)如图2,若点M(-1,1),点A,B在反比例函数y=$\frac{k}{x}$(k>0)图象上,且MA=MB,则△MCD是等腰直角三角形,请说明理由.
(3)接问题(2),取CD的中点N,则对任意等腰△MAB,中点N必在一条直线上,请简要说明理由,并直接写出这条直线的解析式.
分析 (1)①设A(a,$\frac{k}{a}$),B(b,$\frac{k}{b}$),用a,b表示出 $\frac{GF}{AG}$与 $\frac{GE}{GB}$的值,故可得出△EGF∽△AGB,所以∠GEF=∠ABG,由此可得出EF∥AB;
②由①可得出四边形ACEF是平行四边形,故AC=EF,同理可得出结论;
(2)过点M作MP⊥x轴于点P,MQ⊥y轴于点Q,根据M点的坐标可知MA=MB,再由SAS定理可得出,△ACM≌△BDM(SAS),故MC=MD.由HL定理得出△CMQ≌△DMP,故∠MCQ=∠MDP,再根据∠CDO+∠DCO=90°可得出CDM+∠MCD=90°,即∠CMD=90°,由此可得出结论;
(3)根据双曲线是以直线y=x为对称轴的轴对称图形,当点M在原点的时候,对于任意等腰△MAB,其中点N必在直线y=x上,当点M不在原点时,其中点N也必在一条定直线上,再由M点的坐标即可得出结论.
解答  解:(1)①如图1,设A(a,$\frac{k}{a}$),B(b,$\frac{k}{b}$),则AG=$\frac{k}{a}$-$\frac{k}{b}$,GF=$\frac{k}{b}$,GE=a,BG=b-a
解:(1)①如图1,设A(a,$\frac{k}{a}$),B(b,$\frac{k}{b}$),则AG=$\frac{k}{a}$-$\frac{k}{b}$,GF=$\frac{k}{b}$,GE=a,BG=b-a
∵$\frac{GF}{AG}$=$\frac{k}{b}$:($\frac{k}{a}$-$\frac{k}{b}$)=$\frac{a}{b-a}$,$\frac{GE}{GB}$=$\frac{a}{b-a}$,
∴$\frac{GF}{AG}$=$\frac{GE}{GB}$.
又∵∠EGF=∠AGB=90°,
∴△EGF∽△AGB,
∴∠GEF=∠ABG,
∴EF∥AB;
②∵EF∥AB,CE∥AF,
∴四边形ACEF是平行四边形,
∴AC=EF,
同理:BD=EF,
∴AC=BD;
(2)如图2,过点M作MP⊥x轴于点P,MQ⊥y轴于点Q,
∴MA=MB,
∴∠MAB=∠MBA,
∴∠MAC=∠MBD.
在△ACM与△BDM中,
∵$\left\{\begin{array}{l}AC=BD\\∠MAC=∠MBD\\ MA=MB\end{array}\right.$,
∴△ACM≌△BDM(SAS)
∴MC=MD.
∵M(-1,1),
∴MP=MQ.
在△CMQ与△DMP中,
∵$\left\{\begin{array}{l}MC=MD\\ MP=MD\end{array}\right.$,
∴△CMQ≌△DMP(HL),
∴∠MCQ=∠MDP,
∵∠CDO+∠DCO=90°,
∴∠CDM+∠MDP+∠MCD-∠MCQ=90°,
∴∠CDM+∠MCD=90°,即∠CMD=90°,
∴△MCD是等腰直角三角形;
(3)∵双曲线是以直线y=x为对称轴的轴对称图形,
∴当点M在原点的时候,对于任意等腰△MAB,其中点N必在直线y=x上,当点M不在原点时,其中点N也必在一条定直线上.
∴此直线平行于直线y=x且必过点M,
∴这条直线是:y=x+1.
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、平行四边形的判定与性质、全等三角形的判定与性质等知识,难度较大.

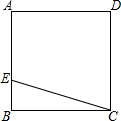 如图,ABCD是一块正方形的场地,小华和小芳在AB边上选定了一点E,测量知EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
如图,ABCD是一块正方形的场地,小华和小芳在AB边上选定了一点E,测量知EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?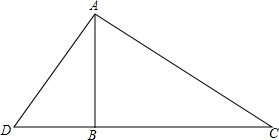 如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长?
如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长?