题目内容

18．若干根火柴恰好可拼成如图1所示的每列2个小正方形共x列，还可拼成如图2所示的每列3个小正方形共y列，那么用含x的代数式表示y，则y=$\frac{5x-1}{7}$．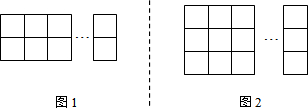

分析 仔细观察两个图形，用代数式表示出两个图形中的图形的个数，从而得到有关x、y的等式，整理即可．

解答 解：如图1，每列的火柴有7根，但两列之间有2根重叠，
∴图1中有火柴7x-2（x-1）=5x+2根；
如图2，每列的火柴有10根，但两列之间有3根重叠，
∴图2中有火柴10y-3（y-1）=7y+3根，
即7y+3=5x+2，
故y=$\frac{5x-1}{7}$．
故答案为：$\frac{5x-1}{7}$．

点评 本题考查了函数关系式，图形的变化类问题，解题的关键是仔细观察图形，发现规律，难度中等．

练习册系列答案
相关题目
3．如图1，已知点A，B是反比例函数y=$\frac{k}{x}$（k＞0）图象上的任意两点，过点A，B作直线交y轴于点C，交x轴于点D．

（1）过点A作AF⊥x轴于点F，过点B作BE⊥y轴于点E，连接EF，请说明：①EF∥AB；②AC=BD；
（2）如图2，若点M（-1，1），点A，B在反比例函数y=$\frac{k}{x}$（k＞0）图象上，且MA=MB，则△MCD是等腰直角三角形，请说明理由．
（3）接问题（2），取CD的中点N，则对任意等腰△MAB，中点N必在一条直线上，请简要说明理由，并直接写出这条直线的解析式．
4．因式分解：（a+b）2+6（a+b）+9．
6．如图，已知半径为$\sqrt{3}$的⊙P的圆心P在直线y=$\sqrt{3}$x上运动．
（1）当⊙P与坐标轴只有一个公共点时，求这个公共点的坐标．
（2）当⊙P与坐标轴有且只有三个公共点时，求圆心P与原点O之间的距离．
（3）当⊙P与坐标轴有4个公共点时．
①直接指出点P的横坐标的取值范围；
②设⊙P与x轴的交点为E，F，点P到y轴的距离为a，试用含a的代数式表示E，F的坐标．
13．如图，P是反比例函数y=$\frac{k}{x}$（x＞0）图象上一动点，PA⊥x轴于A，PB⊥y轴于B，直线l：y=-x+m（m＞0）交x轴、y轴于C、D，交线段PA、PB于E、F，S矩形PAOB=8．
（1）求反比例函数的解析式；
（2）求DE•CF的值；
（3）将直线l平移，使l经过B点，直线l交x轴于G点，交PA于H点，M是GH的中点，连接PM、OM，在P点运动的过程中，$\frac{PM}{OM}$的值是否改变？如果变化，请说明理由；如果不变，请求其值．
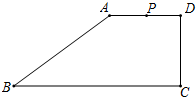3．已知在梯形ABCD中，AD∥BC，∠ADC=90°，且AD=DC=3cm，AB=5cm，动点P从A点出发，以1cm/s的速度沿折线A-D-C运动，过点P作PQ∥AB，交BC于点Q，设运动时间为t（s），
（1）当点P经过CD的中点时，直线PQ与AD的延长线相交于点E，求证：△CPQ≌△DPE．
（2）当△APQ为直角三角形时，求t的值．
10．若双曲线y=$\frac{k-1}{x}$的图象经过第二、四象限，则k的取值范围是（　　）
A．k＞1B．k＜1C．k=1D．不存在
7．若x1、x2为关于x的一元二次方程x2-8x+k+3=0的两个实数根，且满足x1=3x2，试求出方程的两个实数根及k的值．
8．在投掷一枚硬币的试验中，共投掷了100次，其中“正面朝上”的频数为52，则“正面朝上”的频率为0.52．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网