题目内容
14.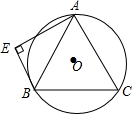 如图,等边△ABC内接于⊙O,BE与⊙O相切于点B,AE⊥BE,⊙O的半径为10,求AE的长.
如图,等边△ABC内接于⊙O,BE与⊙O相切于点B,AE⊥BE,⊙O的半径为10,求AE的长.
分析 如图所示:连接OA、OB,过点O作OD⊥AE,垂足为D,先证明四边形OBED是正方形,从而得到ED=OB=6,∠BOD=90°,然后证明∠AOB=120°,从而得到∠DOA=30°于是得到DA=$\frac{1}{2}AO=3$.
解答 解:如图所示:连接OA、OB,过点O作OD⊥AE,垂足为D.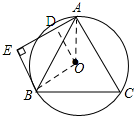
∵BE是圆O的切线,
∴OB⊥BE.
又∵AE⊥BE,OD⊥AE,
∴四边形OBED是矩形.
又∵OD=OB,
∴四边形OBED是正方形.
∴ED=OB=6,∠BOD=90°.
∵△ABC是等边三角形,
∴∠C=60°.
∴∠AOB=120°.
∴∠DOA=30°.
∵在Rt△DAO中,∠DOA=30°,
∴DA=$\frac{1}{2}AO=3$.
∴AE=DE+DA=6+3=9.
点评 本题主要考查的是切线的性质、正方形的判定、等边三角形的性质、圆周角定理,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且AD⊥AB,求证:BC=AB+CD.
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且AD⊥AB,求证:BC=AB+CD.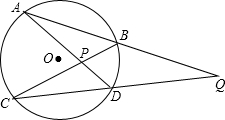 如图,⊙O的弦AB,CD的延长线相交于点Q,AD,CB相交于点P,试探索∠APC及∠Q的度数分别与$\widehat{AC}$和$\widehat{BD}$的度数有怎样的关系,并证明你的结论.
如图,⊙O的弦AB,CD的延长线相交于点Q,AD,CB相交于点P,试探索∠APC及∠Q的度数分别与$\widehat{AC}$和$\widehat{BD}$的度数有怎样的关系,并证明你的结论.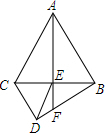 如图所示,△ACB,△ECD是等边三角形,且E点在BC上,AE的延长线交DB于F点,请你在图中找出一对全等三角形,并写出证明它们全等的过程.
如图所示,△ACB,△ECD是等边三角形,且E点在BC上,AE的延长线交DB于F点,请你在图中找出一对全等三角形,并写出证明它们全等的过程.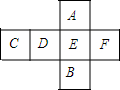 如图,是一个棱柱的平面展开图,每个面上都标上了字母,请根据要求回答下列问题.
如图,是一个棱柱的平面展开图,每个面上都标上了字母,请根据要求回答下列问题.
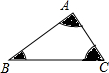 已知∠A+∠B+∠C=180°,分别以点A,B,C为顶点,1为直径画扇形,如图所示,阴影部分的面积为$\frac{π}{8}$.
已知∠A+∠B+∠C=180°,分别以点A,B,C为顶点,1为直径画扇形,如图所示,阴影部分的面积为$\frac{π}{8}$.