题目内容
5.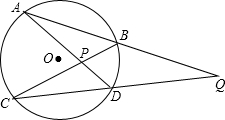 如图,⊙O的弦AB,CD的延长线相交于点Q,AD,CB相交于点P,试探索∠APC及∠Q的度数分别与$\widehat{AC}$和$\widehat{BD}$的度数有怎样的关系,并证明你的结论.
如图,⊙O的弦AB,CD的延长线相交于点Q,AD,CB相交于点P,试探索∠APC及∠Q的度数分别与$\widehat{AC}$和$\widehat{BD}$的度数有怎样的关系,并证明你的结论.
分析 由三角形的外角性质得出∠APC=∠ABC+∠BAD,即可得出结果;由三角形的外角性质和圆周角定理得出∠Q=∠ADC-∠BAD,即可得出结果.
解答 解:∠APC=$\frac{1}{2}$($\widehat{AC}$+$\widehat{BD}$)的度数,∠Q=$\frac{1}{2}$($\widehat{AC}$-$\widehat{BD}$)的度数.理由如下:
∵∠APC=∠ABC+∠BAD=∠ABC=$\frac{1}{2}\widehat{AC}$的度数+$\frac{1}{2}$$\widehat{BD}$的度数,
∴∠APC=$\frac{1}{2}$($\widehat{AC}$+$\widehat{BD}$)的度数;
∵∠ADC=∠Q+∠BAD,
∴∠Q=∠ADC-∠BAD═$\frac{1}{2}\widehat{AC}$的度数-$\frac{1}{2}$$\widehat{BD}$的度数,
∴∠Q=$\frac{1}{2}$($\widehat{AC}$-$\widehat{BD}$)的度数.
点评 本题考查了圆周角定理、三角形的外角性质;熟练掌握圆周角定理和三角形的外角性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,长方形ABCD的对角线AC与BD相交于点O,以O为原点建立直角坐标系,使x轴和y轴分别与长方形两邻边平行.已知AD=9,AB=4,求:
如图,长方形ABCD的对角线AC与BD相交于点O,以O为原点建立直角坐标系,使x轴和y轴分别与长方形两邻边平行.已知AD=9,AB=4,求: 如图,△ABC内接⊙O中,AB=AC=5cm,BC=6cm,求⊙O的半径.
如图,△ABC内接⊙O中,AB=AC=5cm,BC=6cm,求⊙O的半径. 如图,直线AB,CD,EF相交于O
如图,直线AB,CD,EF相交于O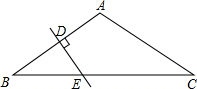 如图,在△ABC中,∠A=120°,AB=AC,AB的垂直平分线DE与AB,BC分别交于点D和E.若BE=3,试求CE的长.
如图,在△ABC中,∠A=120°,AB=AC,AB的垂直平分线DE与AB,BC分别交于点D和E.若BE=3,试求CE的长. 如图,圆内接正五边形ABCDE中,对角线AC和BE相交于圆内的点P,求证:△APB为等腰三角形.
如图,圆内接正五边形ABCDE中,对角线AC和BE相交于圆内的点P,求证:△APB为等腰三角形.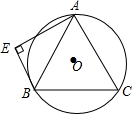 如图,等边△ABC内接于⊙O,BE与⊙O相切于点B,AE⊥BE,⊙O的半径为10,求AE的长.
如图,等边△ABC内接于⊙O,BE与⊙O相切于点B,AE⊥BE,⊙O的半径为10,求AE的长.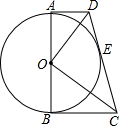 如图,AB是⊙O的直径,AD、BC、CD分别与⊙O相切于A、B、E,则:
如图,AB是⊙O的直径,AD、BC、CD分别与⊙O相切于A、B、E,则: