题目内容
4.解方程:(1)x2-4x+1=0
(2)2x2+5x-3=0.
分析 (1)先把常数项移到等号的右边,再在等式的两边同时加上一次项系数一半的平方,配成完全平方的形式,再开方即可;
(2)先找出a,b及c的值,再代入求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$,进行计算即可.
解答 解:(1)x2-4x+1=0
x2-4x=-1,
x2-4x+4=-1+4,
(x-2)2=3,
x-2=±$\sqrt{3}$,
x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$;
(2)2x2+5x-3=0,
∵a=2,b=5,c=-3,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-5±\sqrt{25+24}}{4}$=$\frac{-5±7}{4}$,
∴x1=-3,x2=$\frac{1}{2}$.
点评 本题考查了解一元二次方程的方法,掌握配方法的步骤和求根公式是本题的关键,配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方;求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
12.下列各数中是无理数的是( )
| A. | 3.14 | B. | $\frac{1}{3}$ | C. | $\sqrt{36}$ | D. | -$\sqrt{3}$ |
19.下列四组线段中,能构成比例线段的一组是( )
| A. | 1cm,3cm,3cm,6cm | B. | 2cm,3cm,4cm,6cm | ||
| C. | 1cm,$\sqrt{2}$cm,$\sqrt{3}$cm,$\sqrt{5}$cm | D. | 1cm,1.5cm,3cm,4cm |
9. 一个正方体的平面展开图如图所示,将它折成正方体后,“崇”字对面的字是(( )
一个正方体的平面展开图如图所示,将它折成正方体后,“崇”字对面的字是(( )
 一个正方体的平面展开图如图所示,将它折成正方体后,“崇”字对面的字是(( )
一个正方体的平面展开图如图所示,将它折成正方体后,“崇”字对面的字是(( )| A. | 低 | B. | 碳 | C. | 生 | D. | 活 |
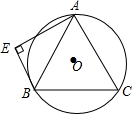 如图,等边△ABC内接于⊙O,BE与⊙O相切于点B,AE⊥BE,⊙O的半径为10,求AE的长.
如图,等边△ABC内接于⊙O,BE与⊙O相切于点B,AE⊥BE,⊙O的半径为10,求AE的长.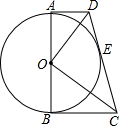 如图,AB是⊙O的直径,AD、BC、CD分别与⊙O相切于A、B、E,则:
如图,AB是⊙O的直径,AD、BC、CD分别与⊙O相切于A、B、E,则: