题目内容
20.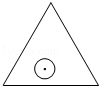 如图,一个半径为r的圆形纸片在边长为a$(a≥2\sqrt{3}r)$的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
如图,一个半径为r的圆形纸片在边长为a$(a≥2\sqrt{3}r)$的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )| A. | $(3\sqrt{3}-π){r^2}$ | B. | $\frac{{(3\sqrt{3}-π)}}{3}{r^2}$ | C. | $\frac{π}{3}{r^2}$ | D. | πr2 |
分析 过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,连AO1,则在Rt△ADO1中,可求得AD=$\sqrt{3}$r.四边形ADO1E的面积等于三角形ADO1的面积的2倍,还可求出扇形O1DE的面积,所求面积等于四边形ADO1E的面积减去扇形O1DE的面积的三倍.
解答 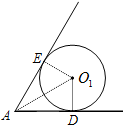 解:如图,当圆形纸片运动到与∠A的两边相切的位置时,
解:如图,当圆形纸片运动到与∠A的两边相切的位置时,
过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,
连AO1,则Rt△ADO1中,∠O1AD=30°,O1D=r,AD=$\sqrt{3}$r.
则S△ADO1=$\frac{1}{2}$O1D•AD=$\frac{\sqrt{3}}{2}$r2,S四边形ADO1E=2S△ADO1=$\sqrt{3}$r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=$\frac{π}{3}$r2,
∴圆形纸片不能接触到的部分的面积为3($\sqrt{3}$r2-$\frac{π}{3}$r2)=(3$\sqrt{3}$-π)r2.
故选:A.
点评 本题考查了轨迹,扇形面积的计算、等边三角形的性质和切线的性质,求出四边形ADO1E的面积与扇形O1DE的面积是解题的关键.

练习册系列答案
相关题目
15.若点(5,2)在一次函数y=kx-3(k≠0)的图象上,则k的值是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
12.在分式$\frac{b}{a+2b}$中,如果a、b都扩大为原来的3倍,则分式的值将( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
9.如图,∠1与∠2不是同旁内角的是( )
| A. | 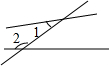 | B. |  | C. | 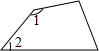 | D. | 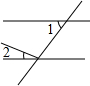 |
10.下列计算正确的是( )
| A. | $\sqrt{(-1)^{2}}$=-2 | B. | a2+a5=a7 | C. | (a2)5=a10 | D. | $\sqrt{5}$×2$\sqrt{5}$=12$\sqrt{5}$ |
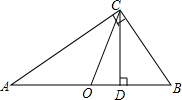 如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.
如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.