��Ŀ����
6����ͼ1���ڡ�ABC�У���A=30�㣬��P�ӵ�A������2cm/s���ٶ�������A-C-B�˶�����Q�ӵ�A������a��cm/s�����ٶ���AB�˶���P��Q����ͬʱ��������ijһ���˶�����Bʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊx��s������APQ�����Ϊy��cm2����y����x�ĺ���ͼ����C1��C2������ɣ���ͼ2��ʾ��
��1����a��ֵ��
��2����ͼ2��ͼ��C2�εĺ�������ʽ��
��3������P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ���������x��ȡֵ��Χ��
���� ��1����PD��AB��D������ֱ�������ε����ʵõ�PD=$\frac{1}{2}$AP=x�����������ε������ʽ�õ���������ʽ��������㣻
��2�����ݵ�x=4ʱ��y=$\frac{4}{3}$�����sinB���õ�ͼ��C2�εĺ�������ʽ��
��3�����y=$\frac{1}{2}$x2�����ֵ�����ݶ��κ��������ʼ��㼴�ɣ�
��� �⣺��1�� ��ͼ1����PD��AB��D��
��ͼ1����PD��AB��D��
�ߡ�A=30�㣬
��PD=$\frac{1}{2}$AP=x��
��y=$\frac{1}{2}$AQ•PD=$\frac{1}{2}$ax2��
��ͼ���֪����x=1ʱ��y=$\frac{1}{2}$��
��$\frac{1}{2}$��a��12=$\frac{1}{2}$��
��ã�a=1��
��2�� ��ͼ2��
��ͼ2��
�ɣ�1��֪����Q���ٶ���1cm/s��
��AC+BC��2AB������P���ٶ�ʱ2cm/s�����Ե�P�ȵ���B�㣬
��PD��AB��D��
��ͼ���֪��PB=5��2-2x=10-2x��
PD=PB•sinB=��10-2x��•sinB��
��y=$\frac{1}{2}$��AQ��PD=$\frac{1}{2}$x����10-2x��•sinB��
�ߵ�x=4ʱ��y=$\frac{4}{3}$��
��$\frac{1}{2}$��4����10-2��4��•sinB=$\frac{4}{3}$��
��ã�sinB=$\frac{1}{3}$��
��y=$\frac{1}{2}$x����10-2x����$\frac{1}{3}$=-$\frac{1}{3}$x2+$\frac{5}{3}$x��
��3��$\frac{1}{2}$x2=-$\frac{1}{3}$x2+$\frac{5}{3}$x��
��ã�x1=0��x2=2��
��ͼ���֪����x=2ʱ��y=$\frac{1}{2}$x2�����ֵ�����ֵ��$\frac{1}{2}$��22=2��
-$\frac{1}{3}$x2+$\frac{5}{3}$x=2��
��ã�x1=3��x2=2��
�൱2��x��3ʱ����P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ�������
���� ���⿼����������ε�������㡢���κ����Ľ���ʽ��ȷ�������κ��������ʣ�����ͼ��ȷ��x���˶�ʱ��������Ĺ�ϵ�ǽ���Ĺؼ���

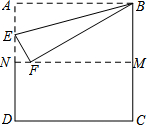 ��ͼ���ѱ߳�Ϊ2��������ֽƬABCD�ȶ���һ����չ�����ۺ�ΪMN��Ȼ�����ع���B���߶��۵���ʹ�õ�A����MN�ϵĵ�F�����ۺ۽�AN�ڵ�E����NF�ij�Ϊ��������
��ͼ���ѱ߳�Ϊ2��������ֽƬABCD�ȶ���һ����չ�����ۺ�ΪMN��Ȼ�����ع���B���߶��۵���ʹ�õ�A����MN�ϵĵ�F�����ۺ۽�AN�ڵ�E����NF�ij�Ϊ��������| A�� | 2 | B�� | 2-$\sqrt{3}$ | C�� | $\sqrt{2}$-1 | D�� | 1 |
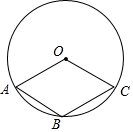 ��ͼ����A��B��C����ԲO�ϣ������ı���OABC�����Σ���ô��O��2��A�Ĺ�ϵ�ǣ�������
��ͼ����A��B��C����ԲO�ϣ������ı���OABC�����Σ���ô��O��2��A�Ĺ�ϵ�ǣ�������| A�� | ��O��2��A | B�� | ��O=2��A | C�� | ��O��2��A | D�� | ����ȷ�� |
 ��ͼ����һ�����ǰ��һ�ŶԱ�ƽ�е�ֽ�������з�ʽ�ڷţ��������ǰ��һֱ�DZ��غϣ���30��ǵ�ֱ�����ǰ��б����ֽ��һ���غϣ���45��ǵ����ǰ��һ��������ֽ������һ���ϣ����1�Ķ����ǣ�������
��ͼ����һ�����ǰ��һ�ŶԱ�ƽ�е�ֽ�������з�ʽ�ڷţ��������ǰ��һֱ�DZ��غϣ���30��ǵ�ֱ�����ǰ��б����ֽ��һ���غϣ���45��ǵ����ǰ��һ��������ֽ������һ���ϣ����1�Ķ����ǣ�������| A�� | 15�� | B�� | 22.5�� | C�� | 30�� | D�� | 45�� |
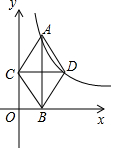 ��ͼ����ֱ������ϵ�У���A�ں���y=$\frac{4}{x}$��x��0����ͼ���ϣ�AB��x���ڵ�B��AB�Ĵ�ֱƽ������y�ύ�ڵ�C���뺯��y=$\frac{4}{x}$��x��0����ͼ���ڵ�D������AC��CB��BD��DA�����ı���ACBD��������ڣ�������
��ͼ����ֱ������ϵ�У���A�ں���y=$\frac{4}{x}$��x��0����ͼ���ϣ�AB��x���ڵ�B��AB�Ĵ�ֱƽ������y�ύ�ڵ�C���뺯��y=$\frac{4}{x}$��x��0����ͼ���ڵ�D������AC��CB��BD��DA�����ı���ACBD��������ڣ�������| A�� | 2 | B�� | 2$\sqrt{3}$ | C�� | 4 | D�� | 4$\sqrt{3}$ |
| A�� | -8 | B�� | 8 | C�� | 16 | D�� | -16 |
 ��ͼ����6��С��������ɵ�2��3�����У�����ѡȡ5��С�����β�Ϳ�ڣ����ɫ���ֵ�ͼ������Գ�ͼ�εĸ�����$\frac{1}{3}$��
��ͼ����6��С��������ɵ�2��3�����У�����ѡȡ5��С�����β�Ϳ�ڣ����ɫ���ֵ�ͼ������Գ�ͼ�εĸ�����$\frac{1}{3}$�� ��ͼ����֪l1��l2��ֱ��l��l1��l2�ཻ��C��D���㣬��һ�麬30��ǵ����dz߰���ͼλ�ðڷţ�����1=130�㣬���2=20�㣮
��ͼ����֪l1��l2��ֱ��l��l1��l2�ཻ��C��D���㣬��һ�麬30��ǵ����dz߰���ͼλ�ðڷţ�����1=130�㣬���2=20�㣮 ��ͼ��б��AC���±�Ϊ0.8��1����BC=5����б��AC=$\sqrt{41}$��
��ͼ��б��AC���±�Ϊ0.8��1����BC=5����б��AC=$\sqrt{41}$��