题目内容
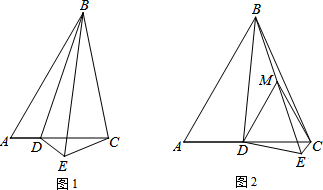
10.如图,在△ABC中,∠A=60°,点D是AC边上一点,连接BD,将△ABD沿DB折叠至△EBD,连接EC,且BE=AC+CE.(1)如图1,求证:∠BEC=$\frac{1}{2}$∠DEC;
(2)如图2,当AD=4EC=4时,在BE上取一点M使MD=MC,求BM的长.
分析 (1)延长AC到F,使CF=CE,从而证得△ABF是等边三角形,得出∠F=60°,BE=BF,然后根据SSS证得△BEC≌△BFC,即可求得∠BEC=∠BED=60°=$\frac{1}{2}$∠DEC;
(2)根据余弦定理可以求得DE,EM的大小关系,根据DE,EM的大小关系,可以求得BM的长,即可解题.
解答 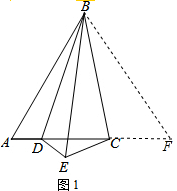 (1)证明:延长AC到F,使CF=CE,如图1,
(1)证明:延长AC到F,使CF=CE,如图1,
∵BE=AC+CE,
∴BE=AC+CF=AF,
∵△ACD≌△EBD,
∴∠BED=∠A=60°,BE=BA,
∴AB=AF,
∴△ABF是等边三角形,
∴∠F=60°,BF=AB=AF,
∴BE=BF,
在△BEC和△BFC中,
$\left\{\begin{array}{l}{BE=BF}\\{CE=CF}\\{BC=BC}\end{array}\right.$,
∴△BEC≌△BFC(SSS),
∴∠BEC=∠BED=60°=$\frac{1}{2}$∠DEC;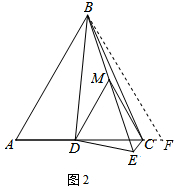
(2)解:延长AC到F,使CF=CE,如图2,
由(1)可知BF=AB=AF,∠BEC=∠BED=60°,
∵DM2=DE2+EM2-2DE•EM•cos60°,
CM2=EC2+EM2-2EC•EM•cos60°,
设DE=x,EM=y,则x2+y2-xy=1+y2-y,
x2-1-(x-1)y=0,
(x-1)(x+1-y)=0,
解得x=1(舍去),y=x+1,
BM=BE-EM=BF-y=BD+4-y=x+4-(x+1)=3.
点评 本题考查了折叠的性质,全等三角形的判定和性质,等边三角形的判定和性质,三角形中余弦定理的使用,作出辅助线构建全等三角形是解题的关键.

练习册系列答案
相关题目
18.已知b<0,则二次根式-$\sqrt{{a}^{3}b}$的化简结果是( )
| A. | -a$\sqrt{-ab}$ | B. | -a$\sqrt{ab}$ | C. | a$\sqrt{ab}$ | D. | a$\sqrt{-ab}$ |
5.x为何值时,$\frac{x}{x-1}$在实数范围内有意义( )
| A. | x>1 | B. | x≥1 | C. | x≠1 | D. | x≤0 |
19.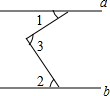 如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
 如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )| A. | 20° | B. | 80° | C. | 100° | D. | 90° |
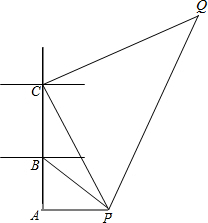 如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.
如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.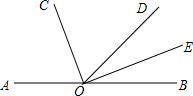 如图,∠AOD与∠BOD互为补角,射线OC、OE分别平分∠AOD和∠BOD.
如图,∠AOD与∠BOD互为补角,射线OC、OE分别平分∠AOD和∠BOD.