题目内容
11．若关于x的一元二次方程x2-4x+（5-m）=0有实数根，则m的取值范围是（ ）| A． | m＞1 | B． | m≥1 | C． | m＜1 | D． | m≤1 |
分析 由方程有实数根，可得知b2-4ac≥0，套入数据得出关于m的一元一次不等式，解不等式即可得出结论．
解答 解：∵方程x2-4x+（5-m）=0有实数根，
∴b2-ac=（-4）2-4（5-m）≥0，
解得：m≥1．
故选B．
点评 本题考查了根的判别式，解题的关键是根据方程有实根得出关于m的一元一次不等式．本题属于基础题，难度不大，解决该题型题目时，根据根的个数由根的判别式得出关于未知数的不等式或不等式组是关键．
练习册系列答案
相关题目
4．
下列条件不能够证明a∥b的是（ ）
下列条件不能够证明a∥b的是（ ）| A． | ∠2+∠3=180° | B． | ∠1=∠4 | C． | ∠2+∠4=180° | D． | ∠2=∠3 |
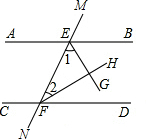如图，直线AB和CD被直线MN所截，EG平分∠BEF，FH平分∠DFE，问：当∠1与∠2互余时，AB与CD有什么位置关系？为什么？