题目内容
2. 如图,将长方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠FBE的度数为20°.
如图,将长方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠FBE的度数为20°.
分析 根据翻折的性质可得∠BEF=∠BEC,∠EBF=∠EBC,然后求出∠BEC,再根据直角三角形两锐角互余求出∠EBC,进而得出∠FBE的度数.
解答 解:由翻折的性质得,∠BEF=∠BEC,∠EBF=∠EBC,
∵∠DEF=40°,
∴∠BEC=$\frac{1}{2}$(180°-∠DEF)=$\frac{1}{2}$(180°-40°)=70°,
∴∠EBC=90°-∠BEC=90°-70°=20°,
即∠FBE=20°,
故答案为:20°.
点评 本题考查了翻折变换的性质,正方形的性质以及平行线的性质的运用,熟记翻折变换前后的图形能够重合是解题的关键.

练习册系列答案
相关题目
17.小明与爸爸的年龄和是52岁,爸爸对小明说:“当我的年龄是你现在的年龄的时候,你还要16年才出生呢.”如果设现在小明的年龄是x岁,爸爸的年龄是y岁,那么下面方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+52=y}\\{x+16=y-x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-x=52}\\{x-16=y-x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=52}\\{y-2x=16}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=52-x}\\{x-16=y-x}\end{array}\right.$ |
11.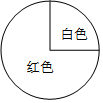 如图,转盘的白色扇形和红色扇形的圆心角分别为90°和270°,让转盘自由转动2次,指针第一次落在红色区域,第二次落在白色区域的概率( )
如图,转盘的白色扇形和红色扇形的圆心角分别为90°和270°,让转盘自由转动2次,指针第一次落在红色区域,第二次落在白色区域的概率( )
 如图,转盘的白色扇形和红色扇形的圆心角分别为90°和270°,让转盘自由转动2次,指针第一次落在红色区域,第二次落在白色区域的概率( )
如图,转盘的白色扇形和红色扇形的圆心角分别为90°和270°,让转盘自由转动2次,指针第一次落在红色区域,第二次落在白色区域的概率( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{16}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{8}$ |
 如图所示,以Rt△ABC的直角边BC为直径向外作半圆,则该半圆的面积为18π.
如图所示,以Rt△ABC的直角边BC为直径向外作半圆,则该半圆的面积为18π.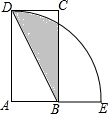 如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$-4.
如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$-4.