题目内容
18．
一次函数y=（m+1）x+2在平面直角坐标系中的图象如图所示，则m的取值范围是（ ）| A． | m＞-1 | B． | m＜-1 | C． | m≥-1 | D． | m≤-1 |
分析 根据图象判断出m+1的符号，再解答即可．
解答 解：由图象可得：m+1＜0，
解得：m＜-1，
故选B
点评 本题考查了一次函数的图象与系数的关系，解题的关键是能够根据图象确定m的符号，难度不大．
练习册系列答案
名校课堂系列答案
相关题目
8．计算：（-$\frac{1}{2}$）×2=（ ）
| A． | -1 | B． | 1 | C． | 4 | D． | -4 |
9．
如图，AB∥CD，以点A为圆心，小于AC长为半径画圆弧，分别交AB、AC于E、F两点：再分别以E、F为圆心，大于$\frac{1}{2}$EF长为半径画圆弧，两弧交于点G，作射线AG交CD于点H．若∠C=150°，则∠AHC大小是（ ）
如图，AB∥CD，以点A为圆心，小于AC长为半径画圆弧，分别交AB、AC于E、F两点：再分别以E、F为圆心，大于$\frac{1}{2}$EF长为半径画圆弧，两弧交于点G，作射线AG交CD于点H．若∠C=150°，则∠AHC大小是（ ）| A． | 15° | B． | 25° | C． | 30° | D． | 35° |
6．
如图，在正方形ABCD中，AB=2，延长AB至点E，使得BE=1，EF⊥AE，EF=AE．分别连接AF，CF，M为CF的中点，则AM的长为（ ）
如图，在正方形ABCD中，AB=2，延长AB至点E，使得BE=1，EF⊥AE，EF=AE．分别连接AF，CF，M为CF的中点，则AM的长为（ ）| A． | 2$\sqrt{2}$ | B． | 3$\sqrt{2}$ | C． | $\frac{11}{4}$ | D． | $\frac{\sqrt{26}}{2}$ |
13．
二次函数y=ax2+bx+c（a≠0）图象如图所示，则下列结论中错误的是（ ）
二次函数y=ax2+bx+c（a≠0）图象如图所示，则下列结论中错误的是（ ）| A． | 当m≠1时，a+b＞am2+bm | |
| B． | 若a${x}_{1}^{2}$+bx1=a${x}_{2}^{2}$+bx2，且x1≠x2，则x1+x2=2 | |
| C． | a-b+c＞0 | |
| D． | abc＜0 |
甲、乙两人骑车分别从A，B两地同时出发，相向而行．两人从出发到相遇共用了6小时，而且两人在此过程中，均改变了一次骑车速度．其中两人行驶路程y（km）与行驶时间x（时）之间的函数图象分别为折线OA-AB与折线OC-CD，如图所示，
10．在Rt△ABC中∠A=90°，BC=10，D为BC的中点．当⊙A半径为6时，则D点与⊙A位置关系为（ ）
| A． | 圆上 | B． | 圆内 | ||
| C． | 圆外 | D． | 以上三种都有可能 |
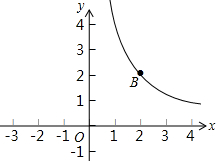在平面直角坐标系xOy中，函数y=$\frac{k}{x}$（k≠0，x＞0）的图象如图所示．已知此图象经过A（m，n），B（2，2）两点．过点B作BD⊥y轴于点D，过点A作AC⊥x轴于点C，AC与BD交于点F．一次函数y=ax+b（a≠0）的图象经过点A、D，与x轴的负半轴交于点E．
8．如图，填在各方格中的三个数之间均具有相同的规律，根据此规律，n的值是（ ）
| A． | 56 | B． | 63 | C． | 70 | D． | 77 |