题目内容
7.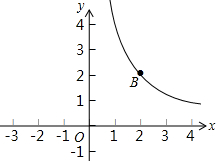 在平面直角坐标系xOy中,函数y=$\frac{k}{x}$(k≠0,x>0)的图象如图所示.已知此图象经过A(m,n),B(2,2)两点.过点B作BD⊥y轴于点D,过点A作AC⊥x轴于点C,AC与BD交于点F.一次函数y=ax+b(a≠0)的图象经过点A、D,与x轴的负半轴交于点E.
在平面直角坐标系xOy中,函数y=$\frac{k}{x}$(k≠0,x>0)的图象如图所示.已知此图象经过A(m,n),B(2,2)两点.过点B作BD⊥y轴于点D,过点A作AC⊥x轴于点C,AC与BD交于点F.一次函数y=ax+b(a≠0)的图象经过点A、D,与x轴的负半轴交于点E.(1)如果AC=$\frac{3}{2}$OD,求a、b的值;
(2)如果BC∥AE,求BC的长.
分析 (1)由点B(2,2)在y=$\frac{k}{x}$的图象上,求得k=4,$y=\frac{4}{x}$,根据已知条件得到A点的坐标为($\frac{4}{3}$,3),解方程组即可得到结论;
(2)设A点的坐标为(m,$\frac{4}{m}$),则C点的坐标为(m,0),推出四边形BCED为平行四边形,根据平行四边形的性质得到CE=BD=2,DE=BC,∠ADF=∠AEC,根据三角函数的定义列方程即可得到结论.
解答  解:(1)如图1,∵点B(2,2)在y=$\frac{k}{x}$的图象上,
解:(1)如图1,∵点B(2,2)在y=$\frac{k}{x}$的图象上,
∴k=4,$y=\frac{4}{x}$,
∵BD⊥y轴,
∴D点的坐标为(0,2),OD=2.
∵AC⊥x轴,AC=$\frac{3}{2}$OD,
∴AC=3,即A点的纵坐标为3,
∵点A在$y=\frac{4}{x}$的图象上,
∴A点的坐标为($\frac{4}{3}$,3),
∵一次函数y=ax+b的图象经过点A、D,
∴$\left\{\begin{array}{l}\frac{4}{3}a+b=3\\ b=2.\end{array}\right.$解得$\left\{\begin{array}{l}a=\frac{3}{4}\\ b=2.\end{array}\right.$
∴a=$\frac{3}{4}$,b=2,
(2)如图2,设A点的坐标为(m,$\frac{4}{m}$),则C点的坐标为(m,0),
∵BD∥CE,且BC∥DE,
∴四边形BCED为平行四边形,
∴CE=BD=2,DE=BC,
∵BD∥CE,
∴∠ADF=∠AEC,
∴在Rt△AFD中,tan∠ADF=$\frac{AF}{DF}=\frac{{\frac{4}{m}-2}}{m}$,
在Rt△ACE中,tan∠AEC=$\frac{AC}{EC}=\frac{{\frac{4}{m}}}{2}$,
∴$\frac{{\frac{4}{m}-2}}{m}=\frac{{\frac{4}{m}}}{2}$,解得m=1,
∴C点的坐标为(1,0),
∴BC=$\sqrt{5}$.
点评 本题考查了反比例函数与一次函数的交点,待定系数法求函数的解析式,平行四边形的判定和性质,三角函数的定义,正确的作出辅助线是解题的关键.

| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
 一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )
一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )| A. | m>-1 | B. | m<-1 | C. | m≥-1 | D. | m≤-1 |
| A. | πcm2 | B. | $\sqrt{3}$πcm2 | C. | 2πcm2 | D. | 4πcm2 |
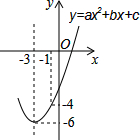 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )| A. | b2>4ac | |
| B. | ax2+bx+c≥-6 | |
| C. | 关于x的一元二次方程ax2+bx+c=-4的两根分别为-5和-1 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
| A. |  | B. |  | C. |  | D. |  |
 如图,在⊙O中,点A为$\widehat{BC}$的中点,若∠BAC=140°,则∠OBA的度数为70°.
如图,在⊙O中,点A为$\widehat{BC}$的中点,若∠BAC=140°,则∠OBA的度数为70°.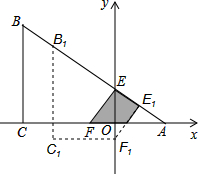 如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.
如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.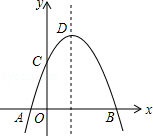 如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题: