题目内容
3. 甲、乙两人骑车分别从A,B两地同时出发,相向而行.两人从出发到相遇共用了6小时,而且两人在此过程中,均改变了一次骑车速度.其中两人行驶路程y(km)与行驶时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD,如图所示,
甲、乙两人骑车分别从A,B两地同时出发,相向而行.两人从出发到相遇共用了6小时,而且两人在此过程中,均改变了一次骑车速度.其中两人行驶路程y(km)与行驶时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD,如图所示,(1)求甲改变前的骑行速度.
(2)求乙改变骑行速度后的y与x之间的函数关系式.
(3)求A,B两地之间的总路程.
分析 (1)直接利用路程÷时间=速度计算;
(2)利用(2,80)和(50,110)求CD的解析式;
(3)先利用(4,80)和(5,110)求AB的解析式,由“相向而行.两人从出发到相遇共用了6小时”,可知,6小时两人的路程和=总路程,据此列式计算.
解答 解:(1)80÷4=20(km/h),
则甲改变前的骑车速度为20km/h;
(2)设CD的解析式为y=kx+b,
将(2,80)和(50,110)代入y=kx+b,得,
$\left\{\begin{array}{l}{2k+b=80}\\{5k+b=110}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=10}\\{b=60}\end{array}\right.$,
∴y乙=10x+60(2≤x≤6);
(3)设甲改变后骑车速度后y与x的关系式为:y=mx+n,
将(4,80)和(5,110)分别代入y=mx+n,
得:$\left\{\begin{array}{l}{4m+n=80}\\{5m+n=110}\end{array}\right.$ 解得$\left\{\begin{array}{l}{m=30}\\{n=-40}\end{array}\right.$,
∴y甲=30x-40(4≤x≤6),
当x=6时,y甲=30×6-40=140,y乙=10×6+60=120,
∴y甲+y乙=140+120=260,
答:A,B两地之间的总路程为260km.
点评 本题考查了一次函数的应用,把一次函数和行程问题结合在一起,关键是能正确利用待定系数法求一次函数的解析式,明确三个量的关系:路程=时间×速度.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
13.下列说法正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 矩形的对角线互相垂直 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 四边相等的四边形是菱形 |
11.在平面直角坐标系中,下列函数的图象经过原点的是( )
| A. | y=-2x+1 | B. | y=-2x | C. | y=-$\frac{2}{x}$ | D. | y=-x2+1 |
18. 一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )
一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )
 一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )
一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )| A. | m>-1 | B. | m<-1 | C. | m≥-1 | D. | m≤-1 |
8.如图,水平放置的几何体中,主视图不是长方形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.一个几何体的主视图和左视图都是边长为2cm的正三角形,俯视图是一个圆,那么这个几何体的侧面积是( )
| A. | πcm2 | B. | $\sqrt{3}$πcm2 | C. | 2πcm2 | D. | 4πcm2 |
12.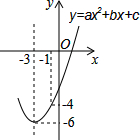 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
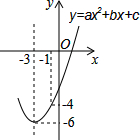 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )| A. | b2>4ac | |
| B. | ax2+bx+c≥-6 | |
| C. | 关于x的一元二次方程ax2+bx+c=-4的两根分别为-5和-1 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
 在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,则△ABC的面积为30.
在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,则△ABC的面积为30.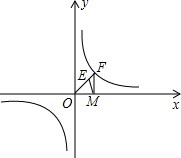 已知:反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(1,1)
已知:反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(1,1)