题目内容
3.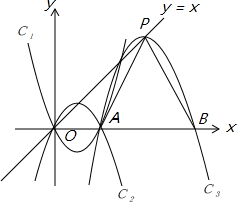 已知抛物线C1的解析式为y=(x-1)2-1,将C1沿x轴翻折得抛物线C2.
已知抛物线C1的解析式为y=(x-1)2-1,将C1沿x轴翻折得抛物线C2.(1)抛物线C2的解析式是:y=-(x-1)2+1;
(2)求抛物线C2与直线y=x的两个交点坐标;
(3)如图,平移抛物线C2得抛物线C3,并且C3顶点P落在直线y=x上,设C3与x轴正半轴交于点A、B,当S△PAB=8时,求抛物线C3的解析式.
分析 (1)根据抛物线C1的解析式为y=(x-1)2-1,将C1沿x轴翻折得抛物线C2,可以求得抛物线C2的解析式;
(2)将抛物线的解析式和直线y=x联立在一起即可解答本题;
(3)根据题意可以求出点P的坐标和点A的坐标,从而可以解答本题.
解答 解:(1)∵抛物线C1的解析式为y=(x-1)2-1,将C1沿x轴翻折得抛物线C2,
∴抛物线C2的解析式是:-y=(x-1)2-1,
即抛物线C2的解析式是:y=-(x-1)2+1,
故答案为:y=-(x-1)2+1;
(2)$\left\{\begin{array}{l}{y=-(x-1)^{2}+1}\\{y=x}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=0}\end{array}\right.,\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=1}\end{array}\right.$,
即抛物线C2与直线y=x的两个交点坐标是(0,0),(1,1);
(3) 设点P的坐标为(a,a),
设点P的坐标为(a,a),
将y=0代入y=-(x-1)2+1,得x=0或x=2,
∴点A的坐标为(2,0),
∴AB的长度为:2(a-2),
∵S△PAB=8,
∴$\frac{2(a-2)•a}{2}=8$,
解得,a=4或a=2(舍去),
∴点P的坐标为(4,4),点A(2,0),
设抛物线C3的解析式是y=m(x-4)2+4,
∵点A(2,0)在抛物线C3的图象上,
∴0=m(2-4)2+4,
解得,m=-1,
∴抛物线C3的解析式是y=-(x-4)2+4.
点评 本题考查抛物线与x轴的交点坐标,一次函数图象上点的坐标特征、二次函数的图象与几何变换,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案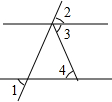 如图,已知∠1=∠2,∠3=65°,则∠4=( )
如图,已知∠1=∠2,∠3=65°,则∠4=( )| A. | 115° | B. | 55° | C. | 25° | D. | 65° |
| A. | $\sqrt{2}×3\sqrt{2}=4\sqrt{2}$ | B. | $\sqrt{24}$$÷\sqrt{6}$=2 | C. | $\sqrt{12}$$+\sqrt{18}$=6$\sqrt{3}$ | D. | $\sqrt{20}$-$\sqrt{5}$=4 |
 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论:
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论: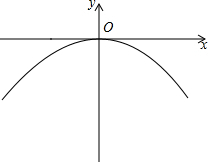 有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.
有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m. 如图是2015年11月的日历.
如图是2015年11月的日历.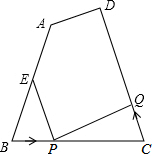 如图,在四边形ABCD中,∠B=∠C,AB=20cm.BC=15cm,点E为AB的中点,如果点P在线段BC上以5cm/秒的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.
如图,在四边形ABCD中,∠B=∠C,AB=20cm.BC=15cm,点E为AB的中点,如果点P在线段BC上以5cm/秒的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.