题目内容
△ABC中,∠A、∠B、∠C所对的边为a、b、c,若a2=c2-b2,则△ABC是 三角形.
考点:勾股定理的逆定理
专题:
分析:根据勾股定理的逆定理解答即可.
解答:解:∵a2=c2-b2,
∴a2+b2=c2,
∴△ABC是直角三角形.
故答案为:直角.
∴a2+b2=c2,
∴△ABC是直角三角形.
故答案为:直角.
点评:本题考查了勾股定理的逆定理,判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
若将抛物线C:y=2x2-4x+1向右平移3个单位得到抛物线C′则抛物线C与C′一定关于某条直线对称,这条直线是( )
A、x=
| ||
| B、x=2 | ||
C、x=
| ||
| D、x=3 |
 如图,直线y=
如图,直线y=| 3 |
| A、(2n,0) |
| B、(n2,0) |
| C、(2n,0) |
| D、(2n-1,0) |
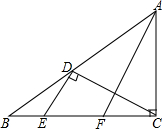 如图,在△ABC中,∠ACB=90°,点D在AB上,AC=AD,DE⊥CD交BC于点E,AF平分∠BAC交BC于F点.
如图,在△ABC中,∠ACB=90°,点D在AB上,AC=AD,DE⊥CD交BC于点E,AF平分∠BAC交BC于F点. 如图,在△ABC中,∠B与∠C的平分线交于点O,过O点作DE∥BC,分别交AB,AC于点D,E.若AB=7,AC=6,则△ADE的周长是
如图,在△ABC中,∠B与∠C的平分线交于点O,过O点作DE∥BC,分别交AB,AC于点D,E.若AB=7,AC=6,则△ADE的周长是 如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.