题目内容
若将抛物线C:y=2x2-4x+1向右平移3个单位得到抛物线C′则抛物线C与C′一定关于某条直线对称,这条直线是( )
A、x=
| ||
| B、x=2 | ||
C、x=
| ||
| D、x=3 |
考点:二次函数图象与几何变换
专题:几何变换
分析:先把y=2x2-4x+1配成顶点式,得到抛物线y=2x2-4x+1的顶点坐标为(1,-1),再根据点平移的规律得到点(1,-1)向右平移3个单位的对应点的坐标为(4,-1),然后通过确定两顶点关于直线x=
对称得到两抛物线关于此直线对称.
| 5 |
| 2 |
解答:解:∵y=2x2-4x+1=2(x-1)2-1,
∴抛物线y=2x2-4x+1的顶点坐标为(1,-1),
∵点(1,-1)向右平移3个单位得到对应点的坐标为(4,-1),
∴抛物线C′的解析式为y=2(x-4)2-1,
∵点(1,-1)与点(4,-1)关于直线x=
对称,
∴抛物线C与C′一定关于直线x=
对称.
故选C.
∴抛物线y=2x2-4x+1的顶点坐标为(1,-1),
∵点(1,-1)向右平移3个单位得到对应点的坐标为(4,-1),
∴抛物线C′的解析式为y=2(x-4)2-1,
∵点(1,-1)与点(4,-1)关于直线x=
| 5 |
| 2 |
∴抛物线C与C′一定关于直线x=
| 5 |
| 2 |
故选C.
点评:本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
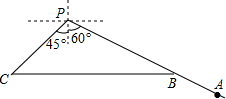 如图,甲船在港口P的南偏西60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向.求乙船的航行速度.(结果精确到个位,参考数据:
如图,甲船在港口P的南偏西60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向.求乙船的航行速度.(结果精确到个位,参考数据:
 如图所示,某住宅社区在相邻两楼之间修建一个上方是一个直径为4m的半圆,下方是一个宽为2.6m的长方形仿古通道,现有一辆卡车装满家具后,高3.9m,宽2.4m,请问这辆送家具的卡车能否通过这个通道?
如图所示,某住宅社区在相邻两楼之间修建一个上方是一个直径为4m的半圆,下方是一个宽为2.6m的长方形仿古通道,现有一辆卡车装满家具后,高3.9m,宽2.4m,请问这辆送家具的卡车能否通过这个通道? 已知:如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=8cm,CE=6cm,则平行四边形ABCD的周长为
已知:如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=8cm,CE=6cm,则平行四边形ABCD的周长为 如图,∠1=∠2,∠3=∠4,∠A=100°,求∠BDC的度数.
如图,∠1=∠2,∠3=∠4,∠A=100°,求∠BDC的度数.