题目内容
有A、C、J、K、S五个球，随机放三个盒里，每个盒放一个球，则K或S在盒中的概率是 ．
考点：列表法与树状图法
专题：
分析：利用排列求出所有的基本事件的个数，再求出K，S都不在盒中的放法，利用古典概型概率公式及对立事件的概率公式求出K或S在盒中的概率．
解答：解：随机放进三个盒子，每个盒子只能放一个球，所有的放法有A53=60，
K，S都不在盒中的放法有A33=6，
设“K或S在盒中”为事件A，
则P（A）=1-
=
，
故答案为：
．
K，S都不在盒中的放法有A33=6，
设“K或S在盒中”为事件A，
则P（A）=1-
| 6 |
| 60 |
| 9 |
| 10 |
故答案为：
| 9 |
| 10 |
点评：本题考查利用排列求事件的个数、古典概型的概率公式、对立事件的概率公式．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
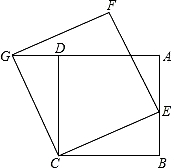如图，已知正方形ABCD，点E是AB上的一点，连接CE，以CE为一边，在CE的上方作正方形CEFG，连接DG．求证：BE=DG．
如图，在菱形ABCD中，过点B作BM⊥AD于点M，BN⊥CD于点N，BM，BN分别交AC于点E、F．求证：AE=CF．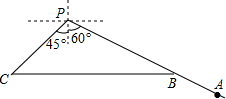
如图，甲船在港口P的南偏西60°方向，距港口30海里的A处，沿AP方向以每小时5海里的速度匀速驶向港口P．乙船从港口P出发，沿南偏东45°方向匀速驶离港口P，现两船同时出发，2小时后甲船到达B处，乙船到达C处，此时乙船恰好在甲船的正西方向．求乙船的航行速度．（结果精确到个位，参考数据：
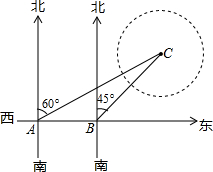在搜索马航MH370的行动中，我国搜救船以80海里/小时的速度由西向东进行搜寻，在A处看见小岛C在船的北偏东60°方向，18分钟后，搜救船行至B处，此时看见小岛C在船的北偏东450方向，已知以小岛C为中心周围30海里以内为珊瑚礁危险区，问这艘搜救船继续向东航行，是否有进入危险区的可能？做重复实验同一枚啤酒瓶盖1000次．经过统计得“凸面向 上”的频率0.48，则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为（ ）
| A、0.24 | B、0.48 |
| C、0.50 | D、0.52 |