题目内容
 如图,一次函数y=-
如图,一次函数y=-| 1 |
| 2 |
| k |
| x |
(1)求b、k的值.
(2)直接写出当x<0时,-
| 1 |
| 2 |
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先将A(-2,0)代入y=-
x+b,求出b=-1,则一次函数解析式为y=-
x-1.设B(x,-
x-1),则x<0,C(x,0),由△ABC的面积为1,列出方程
(-2-x)(-
x-1)=1,解方程求出x的值,得到B点坐标,再把B点坐标代入数y=
,即可求出k的值;
(2)根据图象,在第二象限找出直线y=-
x+b在双曲线y=
上方的部分对应的x的取值即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
(2)根据图象,在第二象限找出直线y=-
| 1 |
| 2 |
| k |
| x |
解答:解:(1)由题意,得A(-2,0).
将A(-2,0)代入y=-
x+b,
得0=-
×(-2)+b,解得b=-1,
则一次函数解析式为y=-
x-1.
设B(x,-
x-1),则x<0,C(x,0),
∵△ABC的面积为1,
∴
(-2-x)(-
x-1)=1,
整理,得
x2+2x=0,
解得x1=-4,x2=0(舍去),
∴B(-4,1).
∵反比例函数y=
的图象经过点B,
∴k=-4×1=-4;
(2)根据图象可知,当x<0时,-
x+b-
>0的解集是x<-4.
将A(-2,0)代入y=-
| 1 |
| 2 |
得0=-
| 1 |
| 2 |
则一次函数解析式为y=-
| 1 |
| 2 |
设B(x,-
| 1 |
| 2 |
∵△ABC的面积为1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
整理,得
| 1 |
| 2 |
解得x1=-4,x2=0(舍去),
∴B(-4,1).
∵反比例函数y=
| k |
| x |
∴k=-4×1=-4;
(2)根据图象可知,当x<0时,-
| 1 |
| 2 |
| k |
| x |
点评:本题考查了反比例函数与一次函数的交点问题,函数图象上点的坐标特征,三角形的面积,利用方程思想及数形结合是解题的关键.

练习册系列答案
相关题目
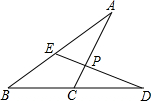 如图所示,已知∠A=20°,∠B=30°,AC⊥DE,求∠BED和∠D的度数.
如图所示,已知∠A=20°,∠B=30°,AC⊥DE,求∠BED和∠D的度数. 直线y=kx-4与x轴、y轴分别交于B、C两点,且
直线y=kx-4与x轴、y轴分别交于B、C两点,且
 如图所示,AB是⊙O的直径,AC是⊙O的弦,∠ACB的平分线交⊙O于点D.若AB=10,AC=6,求BC、BD的长.
如图所示,AB是⊙O的直径,AC是⊙O的弦,∠ACB的平分线交⊙O于点D.若AB=10,AC=6,求BC、BD的长. 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.
如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.