题目内容
10．两地相距600千米，甲乙两车分别从两地同时出发相向而行，甲车比车乙每小时多走10千米，4小时后两车相遇，则乙车的速度是（ ）| A． | 70千米/小时 | B． | 75千米/小时 | C． | 80千米/小时 | D． | 85千米/小时 |
分析 设乙车的速度为x千米/小时，则甲车的速度为（x+10）千米/小时，根据路程=两车速度和×时间即可得出关于x的一元一次方程，解之即可得出结论．
解答 解：设乙车的速度为x千米/小时，则甲车的速度为（x+10）千米/小时，
根据题意得：4（x+x+10）=600，
解得：x=70．
故选A．
点评 本题考查了一元一次方程的应用，根据路程=两车速度和×时间列出关于x的一元一次方程是解题的关键．
练习册系列答案
相关题目
20．为了比较市场上甲乙两种电子钟每日走时误差的情况，从两种电子钟中，各随机抽取10台进行测试，两种电子钟走时误差的数据如表：
（1）计算甲、乙两种电子钟走时误差的平均数；
（2）计算甲、乙两种电子钟走时误差的方差．
| 类型 编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙钟电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
（2）计算甲、乙两种电子钟走时误差的方差．
1．表反映了平面内直线条数与它们最多交点个数的对应关系：
按此规律，6条直线相交，最多有个交点；n条直线相交，最多有$\frac{n（n+1）}{2}$个交点．（n为正整数）
| 图形 |  |  |  | … |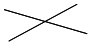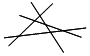
| 直线条数 | 2 | 3 | 4 | … |
| 最多交点个数 | 1 | 3=1+2 | 6=1+2+3 | … |
如图，∠MON=30°，且OP平分∠MON，过点P作PQ∥OM交ON于点Q．若点P到OM的距离为2，则OQ的长为（ ）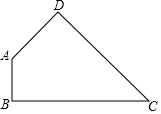
如图，四边形ABCD中，∠ABC=∠ADC=90°，∠C＜90°．点E、F分别是BC、CD上的动点，满足：△AEF的周长最小．
从正面和左面看到长方体的图形如图所示（单位：cm），则从其上面看到图形的面积是12cm2．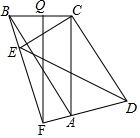
△ABC中，∠ACB=90°，BC=2，AC=4，将△ABC绕C点旋转一个角度到△DEC，直线AD、EB交于F点，在旋转过程中，△ABF的面积的最大值是5．