题目内容
9.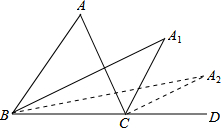 如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2015BC和∠A20l5CD的平分线交于点A2016,则∠A2016=$\frac{m}{{2}^{2016}}$.
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2015BC和∠A20l5CD的平分线交于点A2016,则∠A2016=$\frac{m}{{2}^{2016}}$.
分析 利用角平分线的性质、三角形外角性质,易证∠A1=$\frac{1}{2}$∠A,进而可求∠A1,由于∠A1=$\frac{1}{2}$∠A,∠A2=$\frac{1}{2}$∠A1=$\frac{1}{{2}^{2}}$∠A,…,以此类推可知∠A2016即可求得.
解答 解:∵A1B平分∠ABC,A1C平分∠ACD,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CA=$\frac{1}{2}$∠ACD,
∵∠A1CD=∠A1+∠A1BC,
即$\frac{1}{2}$∠ACD=∠A1+$\frac{1}{2}$∠ABC,
∴∠A1=$\frac{1}{2}$(∠ACD-∠ABC),
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD-∠ABC,
∴∠A1=$\frac{1}{2}$∠A,
∠A2=$\frac{1}{2}$∠A1=$\frac{1}{{2}^{2}}$∠A,…,
以此类推可知∠A2015=$\frac{1}{{2}^{2016}}$∠A=($\frac{m}{{2}^{2016}}$)°,
故答案为:$\frac{m}{{2}^{2016}}$.
点评 本题考查了角平分线性质、三角形外角性质,解题的关键是推导出∠A1=$\frac{1}{2}$∠A,并能找出规律.

练习册系列答案
相关题目
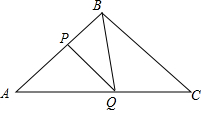 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒. 如图,四边形ABCD∽四边形A′B′C′D′,求边x、y的长度和角α的大小.
如图,四边形ABCD∽四边形A′B′C′D′,求边x、y的长度和角α的大小. 如图所示,若要使AB∥ED,则∠ABC,∠C,∠D应满足什么条件?证明你的结论.
如图所示,若要使AB∥ED,则∠ABC,∠C,∠D应满足什么条件?证明你的结论. 如图,在△ABC中,∠A=45°,直线l与边AB、AC分别交于点M、N,则∠1+∠2的度数是225°.
如图,在△ABC中,∠A=45°,直线l与边AB、AC分别交于点M、N,则∠1+∠2的度数是225°. 已知∠C=90°,四边形CDEF是正方形,AC=15,BC=10,AF与ED交于点G,则EG的长为$\frac{12}{5}$.
已知∠C=90°,四边形CDEF是正方形,AC=15,BC=10,AF与ED交于点G,则EG的长为$\frac{12}{5}$.