题目内容
4.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3“分裂”后,其中有一个奇数是211,则m的值是15.分析 观察规律,分裂成的数都是奇数,且第一个数是底数乘以与底数相邻的前一个数的积再加上1,奇数的个数等于底数,然后找出211所在的奇数的范围,即可得解.
解答 解:∵23=3+5,33=7+9+11,43=13+15+17+19,
…
∴m3分裂后的第一个数是m(m-1)+1,共有m个奇数,
∵15×(15-1)+1=211,
∴奇数211是底数为15的数的立方分裂后的一个奇数,
∴m=15,
故答案为:15
点评 本题是对数字变化规律的考查,找出分裂后的第一个奇数与底数的变化规律是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
13.在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2$\sqrt{2}$,则这个圆锥的侧面积是( )
| A. | 4π | B. | 3π | C. | 2$\sqrt{2}$π | D. | 2π |
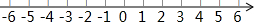 在数轴上表示下列各数,并按从大到小的顺序排列,用“>”连接起来:
在数轴上表示下列各数,并按从大到小的顺序排列,用“>”连接起来: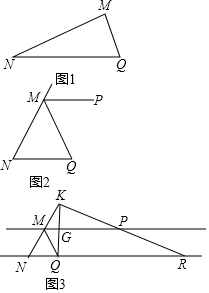 在三角形MNQ中.
在三角形MNQ中.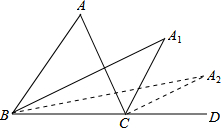 如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2015BC和∠A20l5CD的平分线交于点A2016,则∠A2016=$\frac{m}{{2}^{2016}}$.
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2015BC和∠A20l5CD的平分线交于点A2016,则∠A2016=$\frac{m}{{2}^{2016}}$. 如图,在△ABC中,∠B=70°,∠BAC=45°,AD⊥BC于点D,则∠CAD的度数为25°.
如图,在△ABC中,∠B=70°,∠BAC=45°,AD⊥BC于点D,则∠CAD的度数为25°. 如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E,则∠E=40°.
如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E,则∠E=40°.