题目内容
20.计算:($\frac{1}{81}$)${\;}^{-\frac{1}{4}}$×[(-9)÷($\frac{1}{3}$)-2]${\;}^{-\frac{1}{3}}$.分析 根据负整数指数幂、分数指数幂以及幂的乘方法则进行计算即可.
解答 解:($\frac{1}{81}$)${\;}^{-\frac{1}{4}}$×[(-9)÷($\frac{1}{3}$)-2]${\;}^{-\frac{1}{3}}$
=$({3}^{-4})^{-\frac{1}{4}}$×[(-9)÷9]${\;}^{-\frac{1}{3}}$
=$({3}^{-4})^{-\frac{1}{4}}$×(-1)${\;}^{-\frac{1}{3}}$
=3×(-1)
=-3.
点评 本题主要考查了分数指数幂,负整数指数幂的运用,解题时注意:计算负整数指数幂时,一定要根据负整数指数幂的意义计算,当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.

练习册系列答案
相关题目
8.下列实数中,是无理数的为( )
| A. | $\frac{2}{3}$ | B. | 0 | C. | $\sqrt{36}$ | D. | -π |
15.如图1是边长为a的正三角形,在图1中剪去一个面积最大的矩形得图2,在图2的阴影部分中再分别剪去一个面积最大的矩形得图3…依此类推,则第n个图形中阴影部分的面积为( )
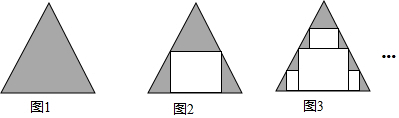

| A. | $\frac{\sqrt{3}}{{2}^{n-1}}{a}^{2}$ | B. | $\frac{\sqrt{3}}{{2}^{n}}{a}^{2}$ | C. | $\frac{\sqrt{3}}{{2}^{n+1}}{a}^{2}$ | D. | $\frac{\sqrt{3}}{{2}^{n+2}}{a}^{2}$ |
5.若sin(α-10o)=$\frac{{\sqrt{3}}}{2}$,则∠α为( )
| A. | 30° | B. | 40° | C. | 60° | D. | 70° |
12.已知正比例函数y=(3m+2)x的图象过点(2,10),则m的取值为( )
| A. | 1 | B. | -1 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
 如图,在四边形ACDB中,AC=CD,∠ACD=∠ABD=90°,∠BCD=30°,BD=$\sqrt{2}$,求BC的长.
如图,在四边形ACDB中,AC=CD,∠ACD=∠ABD=90°,∠BCD=30°,BD=$\sqrt{2}$,求BC的长. 如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为1,则平行四边形ABCD的面积为12.
如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为1,则平行四边形ABCD的面积为12.