题目内容
11.在一个不透明的口袋中,装有分别标有数字2,3,4的3个小球(小球除数字不同外,其余都相同),甲、乙两同学玩摸球游戏,游戏规则如下:先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号,将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数,若该两位数能被4整除,则甲胜,否则乙胜,问这个游戏公平吗?请说明理由.分析 根据题意列出表格,找出被4整除的情况,求出甲乙各自的概率,比较即可判断出游戏得公平性.
解答 解:根据题意列出表格如下:
| 2 | 3 | 4 | |
| 2 | (2,2) | (3,2) | (4,2) |
| 3 | (2,3) | (3,3) | (4,3) |
| 4 | (2,4) | (3,4) | (4,4) |
能被4整除有:24,32,44,即甲胜的概率:$\frac{3}{9}=\frac{1}{3}$,
不能被4整除,即乙胜的概率:$\frac{6}{9}=\frac{2}{3}$,
∵$\frac{1}{3}$<$\frac{2}{3}$
∴不公平
点评 此题考查了统计与概率的知识,根据题意列出表格是解本题的关键.

练习册系列答案
相关题目
6.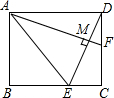 如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
 如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )| A. | $\sqrt{15}$ | B. | $\frac{{\sqrt{15}}}{15}$ | C. | 1 | D. | $\frac{{\sqrt{15}}}{10}$ |
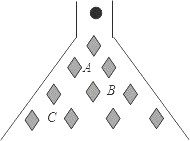 如图所示,当以实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下,求小球下落到第三层B位置的概率$\frac{3}{8}$.
如图所示,当以实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下,求小球下落到第三层B位置的概率$\frac{3}{8}$. 如图,∠ABC=∠ACB.∠ABC、∠ACB的平分线分别交AC、AB于点D、E,且∠1=∠2,试说明CE∥DF.
如图,∠ABC=∠ACB.∠ABC、∠ACB的平分线分别交AC、AB于点D、E,且∠1=∠2,试说明CE∥DF.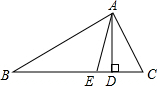 如图,在△ABC中,AD是高,AE是角平分线,∠B=28°,∠C=60°,则∠DAE=16°.
如图,在△ABC中,AD是高,AE是角平分线,∠B=28°,∠C=60°,则∠DAE=16°. 如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.