题目内容
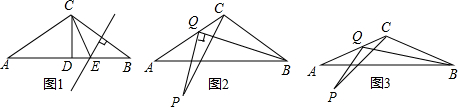
15.如图1是边长为a的正三角形,在图1中剪去一个面积最大的矩形得图2,在图2的阴影部分中再分别剪去一个面积最大的矩形得图3…依此类推,则第n个图形中阴影部分的面积为( )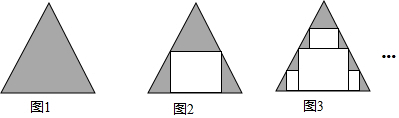
| A. | $\frac{\sqrt{3}}{{2}^{n-1}}{a}^{2}$ | B. | $\frac{\sqrt{3}}{{2}^{n}}{a}^{2}$ | C. | $\frac{\sqrt{3}}{{2}^{n+1}}{a}^{2}$ | D. | $\frac{\sqrt{3}}{{2}^{n+2}}{a}^{2}$ |
分析 如图1,先求出边长为a的等边三角形的面积为:S△ABC=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$a×a=$\frac{\sqrt{3}}{4}{a}^{2}$=$\frac{\sqrt{3}}{{2}^{2}}{a}^{2}$,即是图1阴影图形的面积;
如图2,根据相似表示出内接矩形的面积,由二次函数的最值求出矩形的最大面积,并计算差,即是此时阴影图形的面积;
依此类推,计算第n个图形中阴影部分的面积.
解答 解:如图1,作高线AD,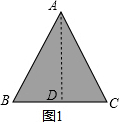
则AD=$\frac{\sqrt{3}}{2}$a,
∴S阴影=S△ABC=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$a×a=$\frac{\sqrt{3}}{4}{a}^{2}$=$\frac{\sqrt{3}}{{2}^{2}}{a}^{2}$,
如图2,作高线AD,交BC于D,交EG于M,
设EG=x,EF=y,
∵EG∥BC,
∴△AEG∽△ABC,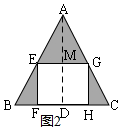
∴$\frac{EG}{BC}=\frac{AM}{AD}$,
∴$\frac{x}{a}=\frac{\frac{\sqrt{3}}{2}a-y}{\frac{\sqrt{3}}{2}a}$,
∴$\frac{\sqrt{3}}{2}$x=$\frac{\sqrt{3}}{2}$a-y,
∴y=$\frac{\sqrt{3}}{2}a-\frac{\sqrt{3}}{2}$x,
∴S矩形EFHG=xy=x($\frac{\sqrt{3}}{2}a-\frac{\sqrt{3}}{2}$x)=-$\frac{\sqrt{3}}{2}{x}^{2}$+$\frac{\sqrt{3}}{2}$ax,
当x=$\frac{\frac{\sqrt{3}}{2}a}{2×\frac{\sqrt{3}}{2}}$=$\frac{1}{2}$a时,S有最大值,S大=-$\frac{\sqrt{3}}{2}$×$(\frac{1}{2}a)^{2}$+$\frac{\sqrt{3}}{2}$a×$(\frac{1}{2}a)$=$\frac{\sqrt{3}}{8}{a}^{2}$,
∴S阴影=$\frac{\sqrt{3}}{4}{a}^{2}$-$\frac{\sqrt{3}}{8}{a}^{2}$=$\frac{\sqrt{3}}{8}{a}^{2}$=$\frac{\sqrt{3}}{{2}^{3}}{a}^{2}$,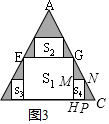
如图3,分别设四个矩形的面积为S1、S2、S3、S4,
由图2可知:EG=$\frac{1}{2}a$,
同理得:S2=$\frac{\sqrt{3}}{8}$×$(\frac{1}{2}a)^{2}$=$\frac{\sqrt{3}}{32}{a}^{2}$,
Rt△GHC中,设MN=m,MH=n,
HC=$\frac{a-\frac{1}{2}a}{2}$=$\frac{1}{4}a$,
∵∠C=60°,
∴∠HGC=30°,
tan30°=$\frac{CH}{GH}$,
∴GH=$\frac{\frac{1}{4}a}{\frac{\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{4}a$,
∵MN∥HC,
∴△GMN∽△GHC,
∴$\frac{MN}{HC}$=$\frac{GM}{GH}$,
∴$\frac{m}{\frac{1}{4}a}$=$\frac{\frac{\sqrt{3}}{4}a-n}{\frac{\sqrt{3}}{4}a}$,
∴n=$\frac{\sqrt{3}}{4}a-\sqrt{3}m$,
∴S4=mn=m($\frac{\sqrt{3}}{4}a-\sqrt{3}m$)=-$\sqrt{3}{m}^{2}$+$\frac{\sqrt{3}}{4}$am,
当m=-$\frac{\frac{\sqrt{3}}{4}a}{2×(-\sqrt{3})}$=$\frac{1}{8}a$时,S4=有最大值,是-$\sqrt{3}$×$(\frac{1}{8}a)^{2}$+$\frac{\sqrt{3}}{4}$a×$\frac{1}{8}$a=$\frac{\sqrt{3}}{64}{a}^{2}$,
∴S阴影=$\frac{\sqrt{3}}{8}{a}^{2}$-2×$\frac{\sqrt{3}}{64}{a}^{2}$-$\frac{\sqrt{3}}{32}{a}^{2}$=$\frac{\sqrt{3}}{16}{a}^{2}$=$\frac{\sqrt{3}}{{2}^{4}}{a}^{2}$,
…
依此类推,则第n个图形中阴影部分的面积为:$\frac{\sqrt{3}}{{2}^{n+1}}{a}^{2}$;
故选C.
点评 本题考查了相似三角形的性质和判定、等边三角形、矩形面积的求法、二次函数的最值问题,有难度,计算量大,熟练掌握相似三角形对应边的比等于对应高的比是关键,与二次函数的相结合,利用二次函数的最值求矩形面积的最大值.

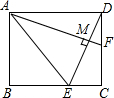 如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )| A. | $\sqrt{15}$ | B. | $\frac{{\sqrt{15}}}{15}$ | C. | 1 | D. | $\frac{{\sqrt{15}}}{10}$ |
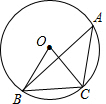 如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=( )
如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=( )| A. | 35° | B. | 45° | C. | 55° | D. | 70° |
| A. | $\frac{200}{x}$=$\frac{200-80}{x+30}$ | B. | $\frac{200}{x}$=$\frac{200-80}{x-30}$ | C. | $\frac{200}{x}$=$\frac{200+80}{x-30}$ | D. | $\frac{200}{x}$=$\frac{200+80}{x+30}$ |
 如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1. 如图,AB是⊙O的弦,过点B的切线与AO的延长线交于点C,如果∠C=58°则∠OAB的度数是16°.
如图,AB是⊙O的弦,过点B的切线与AO的延长线交于点C,如果∠C=58°则∠OAB的度数是16°.