题目内容
8.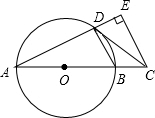 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求⊙O的直径.
分析 (1)连接OD,由切线的性质和圆周角定理可求得∠BDC=∠ADO,再由半径相等可得∠ADO=∠A,可证得结论;
(2)由条件可求得∠DCE=∠A,再利用角的正切值可求得AE,在Rt△ACE中可求得AD,则在Rt△ADB中可求得AB.
解答  (1)证明:
(1)证明:
连接OD,
∵CD是⊙O切线,
∴∠ODC=90°,即∠ODB+∠BDC=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,即∠ODB+∠ADO=90°,
∴∠BDC=∠ADO,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A;
(2)解:
∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∴∠DCE=∠A,
∵CE=4,DE=2,
∴tan∠A=tan∠DCE=$\frac{1}{2}$,
∴在Rt△ACE中,可得AE=8,
∴AD=6,
在在Rt△ADB中 可得BD=3,
∴根据勾股定理可得AB=3$\sqrt{5}$
点评 本题主要考查切线的性质以及圆周角定理、直角三角形的性质等,掌握过切点的半径与切线垂直是解题的关键,注意直角三角形中勾股定理的应用.

练习册系列答案
相关题目
18.在△ABC中,若a=2,b=3,c=4,则△ABC是( )三角形.
| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 无法确定 |
17.两个角,它们的比是7:3,差为36°,则这两个角的关系是( )
| A. | 互余 | B. | 互补 | ||
| C. | 既不互余也不互补 | D. | 不确定 |
18.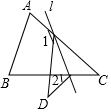 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )| A. | 140° | B. | 90° | C. | 80° | D. | 40° |
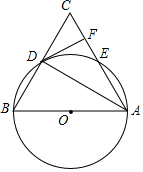 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.
如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.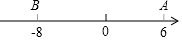 已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上两个动点,点M从A点出发向左运动,速度为每秒2个单位长度,与此同时,点N从B点出发向右运动,速度为M点的3倍,经过多长时间,点M与点N相距50个单位长度?这时点M、N所对应的数分别是多少?
已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上两个动点,点M从A点出发向左运动,速度为每秒2个单位长度,与此同时,点N从B点出发向右运动,速度为M点的3倍,经过多长时间,点M与点N相距50个单位长度?这时点M、N所对应的数分别是多少?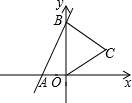 如图,直线y=3x+6与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为(-1,3).
如图,直线y=3x+6与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为(-1,3).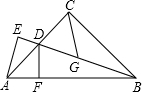 已知:如图,在△ABC中,∠ACB=90°,AC=BC,BD平分∠ABC,BD交AC于点D,过点D作DF⊥AB于点F,过点A作BD的垂线,交BD的延长线于点E,点G是BD的中点.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,BD平分∠ABC,BD交AC于点D,过点D作DF⊥AB于点F,过点A作BD的垂线,交BD的延长线于点E,点G是BD的中点.