题目内容
10.已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )| A. | b2>4ac | |
| B. | 关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 | |
| C. | ax2+bx+c≥-6 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
分析 A:求解析式并化成一般式,计算△=b2-4ac的值;
B:解方程ax2+bx+c=-4,即$\frac{1}{2}$(x+3)2-6=-4;
C:a=$\frac{1}{2}$>0,抛物线的最小值为-6,ax2+bx+c≥-6;
D:看横坐标-2与-5离对称轴x=-3的距离,则-5对应的n>m.
解答 解:设抛物线的解析式为y=a(x+3)2-6,将(-1.-4)代入得:
a(-1+3)2-6=-4,
a=$\frac{1}{2}$,
∴y=$\frac{1}{2}$(x+3)2-6=$\frac{1}{2}{x}^{2}+3x-\frac{3}{2}$,
A:△=b2-4ac=32-4×$\frac{1}{2}$×$(-\frac{3}{2})$>0,所以b2>4ac,故选项A正确;
B:$\frac{1}{2}$(x+3)2-6=-4,
x1=-5,x2=-1,所以$\frac{1}{2}$(x+3)2-6=-4的两根为-5和-1,故选项B正确;
C:抛物线顶点坐标为(-3,-6),即当x=-3时,y有最小值为-6,
所以ax2+bx+c≥-6,故选项C正确;
D:抛物线是轴对称图形,对称轴是x=-3,且a=$\frac{1}{2}$>0,y有最小值为-6,
|-3-(-2)|=1,|-5-(-3)|=2,
所以若点(-2,m),(-5,n)在抛物线上,则m<n,
故选项D错误;
因为本题选择错误的,故选D.
点评 本题综合考查了二次函数的性质,属于基础题,且难度适中;考查了根的判别式、最值与顶点坐标的关系,及一元二次方程与二次函数的关系等几方面的内容.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
20.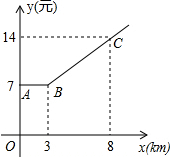 某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
 某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )| A. | 0.71元 | B. | 2.3元 | C. | 1.75元 | D. | 1.4元 |
5.已知直线y=2x+b与坐标轴围成的三角形的面积是4,则b的值是( )
| A. | 4 | B. | 2 | C. | ±4 | D. | ±2 |
19.下列说法正确的是( )
| A. | (3,2)和(2,3)表示同一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(-3,1)到x轴的距离为3 |
 如图所示,直线AB、CD相交于点O,OE⊥AB,OB平分∠DOF,若∠EOC=110°,求∠BOF,∠COF的度数.
如图所示,直线AB、CD相交于点O,OE⊥AB,OB平分∠DOF,若∠EOC=110°,求∠BOF,∠COF的度数.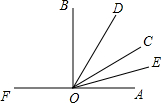 如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC. 如图,已知AB∥CD,若∠C=40°,∠E=20°,求∠A的度数.
如图,已知AB∥CD,若∠C=40°,∠E=20°,求∠A的度数.