题目内容
15．
如图，已知AB∥CD，若∠C=40°，∠E=20°，求∠A的度数．
分析 根据两直线平行，同位角相等可得∠1=∠C，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
解答 
解：如图，∵AB∥CD，
∴∠1=∠C=40°，
∴∠A=∠1-∠E=40°-20°=20°．
点评 本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知函数y1=k1x+b1和y2=k2x+b2交于点（-3，1），k1＞0，k2＜0，如k1x+b1＜k2x+b2，则x的范围为x＜-3．
6．一水库的水位在最近6天内持续上涨，如表记录了这6天的水位高的：
（1）由记录表推出这6天中水位高度h（m）随时间n（天）变化的函数解析式，并画出函数的图象；
（2）据估计这种上涨的势头还会持续2天，预测再过2天水位高度将达到多少米．
| n（天） | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| h（m） | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 |
（2）据估计这种上涨的势头还会持续2天，预测再过2天水位高度将达到多少米．
3．一个观察员要到如图1所示的A，B，C，D四个观测点进行观测，行进路线由在同一平面上的AB，BC，CD，DA，AC，BD组成．为记录观察员的行进路线，在AB的中点M处放置了一台定位仪器，设观察员行进的路程为x，观察员与定位仪器之间的距离为y，若观察员匀速行进，且表示y与x的函数关系的图象大致如图2所示，则观察员的行进路线可能为（ ）
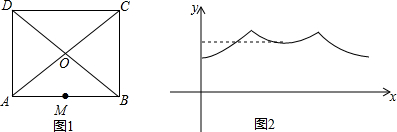
| A． | A→D→C→B | B． | A→B→C→D | C． | A→C→B→D | D． | A→C→D→B |
10．已知顶点为（-3，-6）的抛物线y=ax2+bx+c经过点（-1，-4），则下列结论中错误的是（ ）
| A． | b2＞4ac | |
| B． | 关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 | |
| C． | ax2+bx+c≥-6 | |
| D． | 若点（-2，m），（-5，n）在抛物线上，则m＞n |
20．一蓄水池有水40m3，如果每分钟放出2m3的水，水池里的水量y（m3）与放水时间t（分）有如下关系：
下列结论中正确的是（ ）
| 放水时间（分） | 1 | 2 | 3 | 4 | … |
| 水池中水量（m3） | 38 | 36 | 34 | 32 | … |
| A． | y随t的增加而增大 | |
| B． | 放水时为20分钟时，水池中水量为8m3 | |
| C． | y与t之间的关系式为y=40-t | |
| D． | 放水时为18分钟时，水池中水量为4m3 |
7．
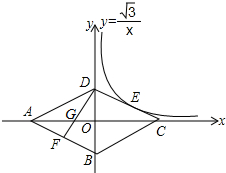如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF⊥AB交AC于点G，反比例函数y=$\frac{\sqrt{3}}{x}$（x＞0）经过线段DC的中点E，若BD=4，则AG的长为（ ）
如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF⊥AB交AC于点G，反比例函数y=$\frac{\sqrt{3}}{x}$（x＞0）经过线段DC的中点E，若BD=4，则AG的长为（ ）| A． | $\frac{4\sqrt{3}}{3}$ | B． | $\sqrt{3}$+2 | C． | 2$\sqrt{3}$+1 | D． | $\frac{3\sqrt{3}}{2}$+1 |
4．当0≤x≤3时，一次函数y=-x+3的最大值是（ ）
| A． | 0 | B． | 3 | C． | -3 | D． | 无法确定 |
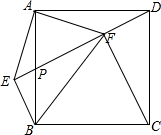如图，在正方形ABCD中，点P是AB的中点，连接DP，过点B作BE⊥DP的延长线于点E，连接AE，过点A作AF⊥AE，AF交DP于点F，连接BF、CF．下列结论：