题目内容
19.下列说法正确的是( )| A. | (3,2)和(2,3)表示同一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(-3,1)到x轴的距离为3 |
分析 (1)有序实数对与坐标平面内的点是一一对应的,一个有序实数对表示一个点,因此(3,2)和(2,3)表示不同的两个点;
(2)纵坐标为0的点在x轴上,且$\sqrt{3}>0$,所以($\sqrt{3}$,0)在x轴的正半轴上;
(3)第二象限上的点的横坐标为正数,纵坐标为负数,所以点(-2,4)在第二象限;
(4)一个点到x轴的距离等于该点纵坐标的绝对值,到y轴的距离等于该点横坐标的绝对值,所以点(-3,1)到x轴的距离为1,到y轴的距离为3.
解答 解:A:(3,2)和(2,3)表示两个点,所以A选项错误;
B:点($\sqrt{3}$,0)在x轴的正半轴上,所以B选项正确;
C:点(-2,4)在第二象限,所以C选项错误;
D:点(-3,1)到x轴的距离为1,所以D选项错误;
故选B.
点评 本题考查了点的坐标,属于基础题,比较简单;熟练掌握平面直角坐标系的相关概念是做好本题的关键:①
各象限点的坐标特征;②坐标轴上点的坐标特征;③坐标平面内的点与有序实数对是一一对应的关系;④点(a,b)到x轴的距离等于|b|,到y轴的距离等于|a|.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
 如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )| A. | (1008,0) | B. | (1008,$\frac{1}{2}$) | C. | (1008,-$\frac{1}{2}$) | D. | (1008π,0) |
10.已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
| A. | b2>4ac | |
| B. | 关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 | |
| C. | ax2+bx+c≥-6 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
7.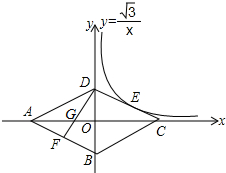 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\sqrt{3}$+2 | C. | 2$\sqrt{3}$+1 | D. | $\frac{3\sqrt{3}}{2}$+1 |
14.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a6÷a3=a2 | C. | 4x3-3x2=1 | D. | (-2x2y)3=-8x6y3 |
4.当0≤x≤3时,一次函数y=-x+3的最大值是( )
| A. | 0 | B. | 3 | C. | -3 | D. | 无法确定 |
 如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )
如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )



 如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.
如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.