题目内容
18.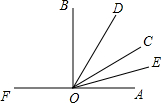 如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.(1)若∠AOE=15°,求∠FOC的度数;
(2)若∠AOB=86°,求∠DOE的度数.
分析 (1)先根据角平分线,求得∠AOC的度数,再根据邻补角求得∠FOC的度数;
(2)先根据角平分线得到∠EOC=$\frac{1}{2}$∠AOC,∠DOC=$\frac{1}{2}$∠BOC,再根据角的和差关系进行计算即可.
解答  解:(1)∵∠AOE=15°,OE平分∠AOC,
解:(1)∵∠AOE=15°,OE平分∠AOC,
∴∠AOC=2×15°=30°,
∵点O是直线FA上一点,
∴∠FOC=180°-30°=150°;
(2)∵OE平分∠AOC,OD平分∠BOC,
∴∠EOC=$\frac{1}{2}$∠AOC,∠DOC=$\frac{1}{2}$∠BOC,
∴∠DOE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×86°=43°.
点评 本题主要考查了角平分线的定义,根据角平分线定义得出所求角与已知角的关系是解决问题的关键.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
9. 如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
 如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )| A. | (1008,0) | B. | (1008,$\frac{1}{2}$) | C. | (1008,-$\frac{1}{2}$) | D. | (1008π,0) |
6.一水库的水位在最近6天内持续上涨,如表记录了这6天的水位高的:
(1)由记录表推出这6天中水位高度h(m)随时间n(天)变化的函数解析式,并画出函数的图象;
(2)据估计这种上涨的势头还会持续2天,预测再过2天水位高度将达到多少米.
| n(天) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| h(m) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 |
(2)据估计这种上涨的势头还会持续2天,预测再过2天水位高度将达到多少米.
3.一个观察员要到如图1所示的A,B,C,D四个观测点进行观测,行进路线由在同一平面上的AB,BC,CD,DA,AC,BD组成.为记录观察员的行进路线,在AB的中点M处放置了一台定位仪器,设观察员行进的路程为x,观察员与定位仪器之间的距离为y,若观察员匀速行进,且表示y与x的函数关系的图象大致如图2所示,则观察员的行进路线可能为( )
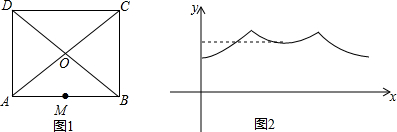

| A. | A→D→C→B | B. | A→B→C→D | C. | A→C→B→D | D. | A→C→D→B |
10.已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
| A. | b2>4ac | |
| B. | 关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 | |
| C. | ax2+bx+c≥-6 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
7.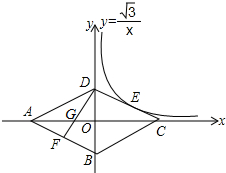 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\sqrt{3}$+2 | C. | 2$\sqrt{3}$+1 | D. | $\frac{3\sqrt{3}}{2}$+1 |
 如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.
如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.