题目内容
20.直线y=$\frac{1}{2}$x+b与函数y=x2+|2x2-1|的图象有且只有三个交点,则b的值为$\frac{1}{2}$+$\frac{\sqrt{2}}{4}$或1+$\frac{\sqrt{2}}{4}$.分析 首先作出函数y=x2+|2x2-1|的图象,根据函数的图象即可确定b的取值.
解答 解:当2x2-1≤0时,即-$\frac{\sqrt{2}}{2}$≤x≤$\frac{\sqrt{2}}{2}$,y=x2+|2x2-1|=-x2+1;
当2x2-1>0时,即x<-$\frac{\sqrt{2}}{2}$或x>$\frac{\sqrt{2}}{2}$,y=x2+|2x2-1|=3x2-1;
作出函数的图象如图: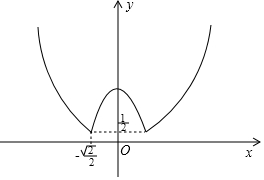
故要使函数y=$\frac{1}{2}$x+b与函数y=x2+|2x2-1|的图象有且只有三个交点,则
$\frac{1}{2}$×(-$\frac{\sqrt{2}}{2}$)+b=$\frac{1}{2}$,解得b=$\frac{1}{2}$+$\frac{\sqrt{2}}{4}$;
或$\frac{1}{2}$×(-$\frac{\sqrt{2}}{2}$)+b=1,解得b=1+$\frac{\sqrt{2}}{4}$.
故b的值为$\frac{1}{2}$+$\frac{\sqrt{2}}{4}$或1+$\frac{\sqrt{2}}{4}$.
故答案为:$\frac{1}{2}$+$\frac{\sqrt{2}}{4}$或1+$\frac{\sqrt{2}}{4}$.
点评 本题考查了二次函数的图象及一次函数的图象,首先作出分段函数的图象是解决本题的关键,采用数形结合的方法确定答案是数学上常用的方法之一.

练习册系列答案
相关题目
10.已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
| A. | b2>4ac | |
| B. | 关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 | |
| C. | ax2+bx+c≥-6 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
 如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )
如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )



 如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.
如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.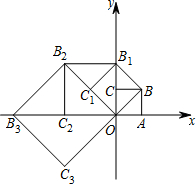 如图,在平面直角坐标系中有一被称为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2020的坐标为(-21010,-21010).
如图,在平面直角坐标系中有一被称为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2020的坐标为(-21010,-21010).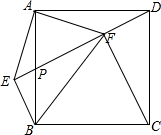 如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:
如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论: