题目内容
5.如图1,我们把形如A、B、C的点叫做网格图的“格点”,顶点在格点上的△ABC叫做格点三角形.(1)在图1上画出△ABC关于点O的中心对称三角形;(点O是矩形网格的中心)
(2)在图2上画出一个与△ABC等面积但不全等的格点三角形;
(3)请你写出图3中所有形如等腰直角三角形的格点三角形的个数.
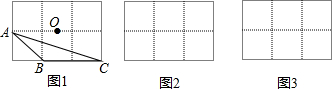
分析 (1)利用网格特点和中心对称的性质画出点A、B、C的对应点A′、B′、C′即可;
(2)利用同底等高三角形的面积相等画格点三角形;
(3)通过确定正方形的个数得到等腰直角三角形:小正方形有6个得到24个等腰直角三角形,大正方形有2个得到24个等腰直角三角形.
解答 解:(1)如图1,△A′B′C′为所作;
(2)如图2,△DBC为所作;
(3)如图3,共有48个等腰直角三角形.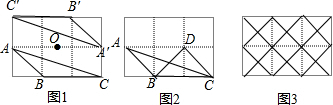
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列各方程中,是一元一次方程的是( )
| A. | x-2y=4 | B. | xy=4 | C. | 3y-1=4 | D. | $\frac{1}{4}x-4$ |
13.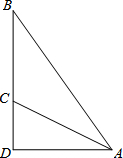 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )| A. | (3+$\sqrt{5}$)米 | B. | 8米 | C. | 6米 | D. | 5米 |
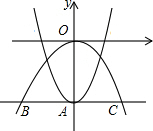 如图,抛物线y=ax2-2与y轴交于点A,过点A与x轴平行的直线交抛物线y=-$\frac{1}{2}$x2于点B,C,则S△BOC=4.
如图,抛物线y=ax2-2与y轴交于点A,过点A与x轴平行的直线交抛物线y=-$\frac{1}{2}$x2于点B,C,则S△BOC=4.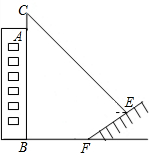 如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)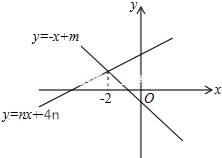 如图,直线y1=-x+m与y2=nx+4n(n≠0)的交点的横坐标为-2,图象可得关于x的不等式组$\left\{\begin{array}{l}{-x+m>nx+4n}\\{nx+4n>0}\end{array}\right.$的解集为-4<x<-2.
如图,直线y1=-x+m与y2=nx+4n(n≠0)的交点的横坐标为-2,图象可得关于x的不等式组$\left\{\begin{array}{l}{-x+m>nx+4n}\\{nx+4n>0}\end{array}\right.$的解集为-4<x<-2.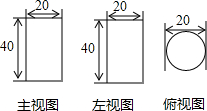 如图,是一个几何体的三视图,它的几何体表面积为900π.
如图,是一个几何体的三视图,它的几何体表面积为900π.