题目内容
9.在Rt△ABC中,若两直角边长为6cm、8cm,则它的外接圆的面积为25πcm2,内切圆的半径为2cm.分析 先根据勾股定理求出AB的长,再由直角三角形外接圆的半径等于斜边的一半可得出外接圆的半径,进而得出其面积.连接OD,OE,由D、E为切点可知OE=OD,故四边形ODCE是正方形,由切线的性质得出BE=BF,AD=AF,根据BF+AF=BE+AD=(8-r)+(6-r)=10,由此可得出r的值.
解答 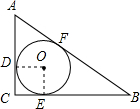 解:如图,∵AC=6cm,BC=8cm,
解:如图,∵AC=6cm,BC=8cm,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10cm,
∴外接圆的半径=5cm,
∴S外接圆=25π(cm2).
连接OD,OE,
∵D、E为切点,
∴OE=OD=r,
∴四边形ODCE是正方形.
∵⊙O是△ABC的内切圆,
∴BE=BF,AD=AF,
∴BF+AF=BE+AD=(8-r)+(6-r)=10,解得r=2cm.
故答案为:25πcm2,2cm.
点评 本题主要考查了三角形的内切圆与外心,切线的性质及勾股定理,关键是能根据题意求出关于内切圆半径的方程.

练习册系列答案
相关题目
13.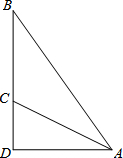 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )| A. | (3+$\sqrt{5}$)米 | B. | 8米 | C. | 6米 | D. | 5米 |
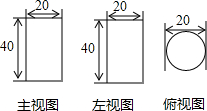 如图,是一个几何体的三视图,它的几何体表面积为900π.
如图,是一个几何体的三视图,它的几何体表面积为900π.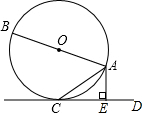 已知:如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AE⊥CD于E,求证:AC2=AE•AB.
已知:如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AE⊥CD于E,求证:AC2=AE•AB.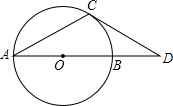 已知,如图AB是⊙O的直径且AB=10,AC是弦,∠A=30°,过C作⊙O的切线交AB延长线于点D,求BD的长.
已知,如图AB是⊙O的直径且AB=10,AC是弦,∠A=30°,过C作⊙O的切线交AB延长线于点D,求BD的长.