题目内容
研究下列算式,你发现了什么规律?(1)1×3+1=4;(2)2×4+1=9;(3)3×5+1=16;(4)4×6+1=25;…第n个等式是: .
考点:规律型:数字的变化类
专题:
分析:由题目中的数据可知1×(1+2)+1=(1+1)2;2×(2+2)+1=(1+2)2;3×(3+2)+1=(1+3)2;所以可据此推出第n个式子为n(n+2)+1=(n+1)2.
解答:解:∵1×(1+2)+1=(1+1)2;2×(2+2)+1=(1+2)2;3×(3+2)+1=(1+3)2;
∴第n个式子为n(n+2)+1=(n+1)2.
故答案为:n(n+2)+1=(n+1)2.
∴第n个式子为n(n+2)+1=(n+1)2.
故答案为:n(n+2)+1=(n+1)2.
点评:此题考查数字的比那话规律,通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.对于等式,要注意分别发现:等式的左边和右边的规律.

练习册系列答案
相关题目
观察下列图形:

请用你发现的规律直接求出图④中的数y和图⑤中的数x,则x+y=( )

请用你发现的规律直接求出图④中的数y和图⑤中的数x,则x+y=( )
| A、10 | B、-14 | C、-12 | D、6 |
已知一定点P与圆周上点的最大距离为6cm,最小距离为2cm,则此圆的半径为( )
| A、4cm |
| B、2cm |
| C、4cm或2cm |
| D、8cm或4cm |
 如图,△ABC和△A1B1C1成轴对称,试作出对称轴.
如图,△ABC和△A1B1C1成轴对称,试作出对称轴.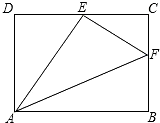 如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在边DC的中点E,折痕为AF,已知CD=8cm.求:
如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在边DC的中点E,折痕为AF,已知CD=8cm.求: 如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.
如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.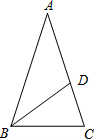 如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.
如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.