题目内容
10.有一列数,a1,a2,a3…an,其中a1=-1,a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$…an=$\frac{1}{1-{a}_{n-1}}$.(1)请分别求出a1,a2,a3的值.
(2)求a1+a2+a3+…+a3n的值(用含n的式子表示).
(3)若a1=2,则a1+a2+a3+…+a3n的值不变(填“改变”或“不变”)
分析 (1)首先根据a1=-1,可得a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-(-1)}=\frac{1}{2}$;然后根据a2=$\frac{1}{2}$,可得a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-\frac{1}{2}}$=2,据此解答即可;
(2)首先根据a1,a2,a3,…的取值情况,找出这列数的排列规律,然后根据数列的求和方法,求出a1+a2+a3+…+a3n的值是多少即可.
(3)若a1=2,根据a1,a2,a3,…的取值情况,找出这列数的排列规律,然后求出a1+a2+a3+…+a3n的值是多少,判断出a1+a2+a3+…+a3n的值改变不改变即可.
解答 解:(1)因为a1=-1,
所以a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-(-1)}=\frac{1}{2}$;
因为a2=$\frac{1}{2}$,
所以a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-\frac{1}{2}}$=2;
(2)因为a3=2,
所以a4=$\frac{1}{1{-a}_{3}}$=$\frac{1}{1-2}$=-1,
所以这列数是:-1、$\frac{1}{2}、2$、-1、$\frac{1}{2}、2、…$,每3个数一个循环:-1、$\frac{1}{2}$、2,
所以a1+a2+a3+…+a3n
=(-1+$\frac{1}{2}$+2)×3n÷3
=$\frac{3}{2}$×3n÷3
=1.5n
(3)若a1=2,
则a2=$\frac{1}{1-2}=-1$,a3=$\frac{1}{2}$,a4=2,a5=-1,…,
所以这列数是:2、-1、$\frac{1}{2}、2$、-1、$\frac{1}{2}、2、…$,从第二个数开始,每3个数一个循环:-1、$\frac{1}{2}$、2,
则a1+a2+a3+…+a3n
=2+(-1+$\frac{1}{2}$+2)×3n÷3-2
=2+$\frac{3}{2}$×3n÷3-2
=2+1.5n-2
=1.5n
所以若a1=2,则a1+a2+a3+…+a3n的值不变.
故答案为:不变.
点评 (1)此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出这列数是:-1、$\frac{1}{2}、2$、-1、$\frac{1}{2}、2、…$,每3个数一个循环:-1、$\frac{1}{2}$、2.
(2)此题还考查了数列的求和问题,要熟练掌握.

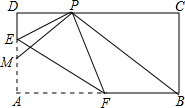 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
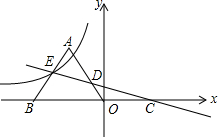 如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )| A. | -$\frac{6}{7}$ | B. | -$\sqrt{3}$ | C. | -3 | D. | -4 |
| A. | x>3 | B. | x≥3 | C. | x=3 | D. | x≠3 |
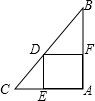 如图,正方形DEAF内接于△ABC,已知AC=8,AB=16,那么正方形的边长是$\frac{16}{3}$.
如图,正方形DEAF内接于△ABC,已知AC=8,AB=16,那么正方形的边长是$\frac{16}{3}$.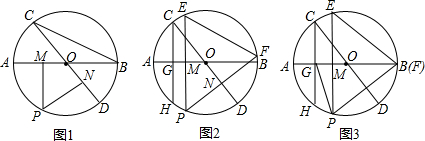
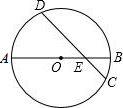 如图,已知⊙O的直径AB与弦CD交于E,∠AED=45°,AB=$\sqrt{2}$,则EC2+ED2=1.
如图,已知⊙O的直径AB与弦CD交于E,∠AED=45°,AB=$\sqrt{2}$,则EC2+ED2=1.