题目内容
19.已知x2+xy-12y2=0,求$\frac{x-4y}{x+5y}$的值.分析 先利用因式分解法得到(x-4y)(x+3y)=0,则x-4y=0或x+3y=0,根据分式有意义的条件得到x+5y≠0,然后把x=4y或x=-3y代入原式进行计算即可.
解答 解:∵x2+xy-12y2=0,
∴(x-4y)(x+3y)=0,
∴x-4y=0或x+3y=0,
∴x=4y或x=-3y,
∵x+5y≠0,
∴当x=4y时,原式=0,
当x=-3y时,原式=-3.5.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
4.有下列方程:①$\frac{3}{x}$-$\frac{4}{y}$=1;②x2-x+$\frac{1}{x}$;③$\frac{1}{a}$-3=1+a;④$\frac{3}{\sqrt{x}}$-x=3,其中属于分式方程的是( )
| A. | ①② | B. | ①③ | C. | ②③④ | D. | ①③④ |
11.下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
| A. | a=1.5,b=2,c=3 | B. | a=7,b=24,c=25 | C. | a=6,b=8,c=10 | D. | a=5,b=12,c=13 |
8.下列各式计算正确的是( )
| A. | 2a+2=3a2 | B. | (-b2)2=-b4 | C. | a2•a3=a5 | D. | (m-n)2=m2-n2 |
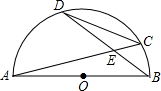 半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=$\frac{27}{5}$,且BD=7,则DE=3$\sqrt{2}$.
半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=$\frac{27}{5}$,且BD=7,则DE=3$\sqrt{2}$.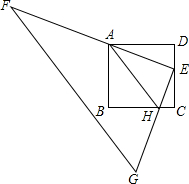 如图,正方形ABCD的边长为4,Rt△FEG的直角顶点E在正方形的边DC上运动,一条直角边EF始终经过点A,另一直角边EG交正方形的边BC于点H;
如图,正方形ABCD的边长为4,Rt△FEG的直角顶点E在正方形的边DC上运动,一条直角边EF始终经过点A,另一直角边EG交正方形的边BC于点H;