题目内容
5.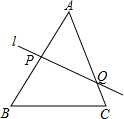 如图,直线l分别交△ABC的边AB、AC于点p、Q,若$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1.则直线1必过△ABC的( )并给予证明.(A)内心;(B)外心;(C)重心;(D)垂心.
如图,直线l分别交△ABC的边AB、AC于点p、Q,若$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1.则直线1必过△ABC的( )并给予证明.(A)内心;(B)外心;(C)重心;(D)垂心.
分析 作△ABC的中线AD,分别过B、C作AD的平行线BE、CF交直线l于点E、F,根据平行线分线段成比例定理、梯形中位线定理得到AH=2DH,得到H为△ABC的重心.
解答  证明:作△ABC的中线AD,分别过B、C作AD的平行线BE、CF交直线l于点E、F,
证明:作△ABC的中线AD,分别过B、C作AD的平行线BE、CF交直线l于点E、F,
∵BE∥DH∥CF,D是BC的中点,
∴DH=$\frac{1}{2}$(CF+BE),
∵BE∥DH,
∴$\frac{BP}{AP}$=$\frac{BE}{AH}$,
∵DH∥CF,
∴$\frac{CQ}{AQ}$=$\frac{CF}{AH}$,
∵$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1,
∴$\frac{BE}{AH}$+$\frac{CF}{AH}$=1,
∴CF+BE=AH,
∴AH=2DH,
∴H为△ABC的重心,
故选:C.
点评 本题考查的是三角形的五心的知识,掌握三角形的重心是三角形三条中线的交点、重心到顶点的距离是到中点的距离的2倍是解题的关键,注意辅助线的作法要正确.

练习册系列答案
相关题目
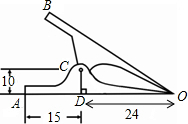 如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15mm,DO=24mm,DC=10mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.
如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15mm,DO=24mm,DC=10mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.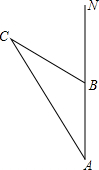 上午6时,一条船从海岛A出发,以15海里/时的速度向正北航行,8时到达海岛B处.从A、B望灯塔C,测得∠NAC=31°,∠NBC=62°,求从海岛B到灯塔C的距离.
上午6时,一条船从海岛A出发,以15海里/时的速度向正北航行,8时到达海岛B处.从A、B望灯塔C,测得∠NAC=31°,∠NBC=62°,求从海岛B到灯塔C的距离.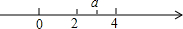 实数a在数轴上的位置如图所示,化简|a-2|+$\sqrt{{a}^{2}-8a+16}$=2.
实数a在数轴上的位置如图所示,化简|a-2|+$\sqrt{{a}^{2}-8a+16}$=2. 如图,Rt△ABC的斜边AB=25,cosA=$\frac{3}{5}$.求BC的长.
如图,Rt△ABC的斜边AB=25,cosA=$\frac{3}{5}$.求BC的长.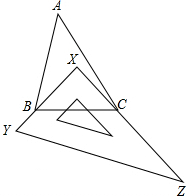 如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.