题目内容
17.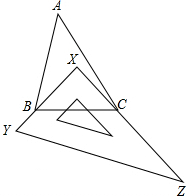 如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角板的位置,但仍使点B,点C在三角板的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
分析 (1)在△ABC中,利用三角形内角和得出∠ABC+∠ACB=180°-∠A,即可求∠ABC+∠ACB;同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB=90°,即可得出结果;
(2)在△ABC中,∠ABC+∠ACB=180°-∠A是一个定值,同理在△XBC中,∠BXC=90°,∠XBC+∠XCB=90°也是一个定值,∠ABX+∠ACX=90°-∠A的值不变.
解答 解:(1)∵∠A=30°,
∴∠ABC+∠ACB=180°-∠A=180°-30°=150°,
∵∠YXZ=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=150°-90°=60°;
(2)∠ABX+∠ACX的大小没有变化;理由如下:
∵∠ABC+∠ACB=180°-∠A,∠YXZ=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=180°-∠A-90°=90°-∠A;
即∠ABX+∠ACX的大小没有变化.
点评 本题考查了三角形内角和定理、直角三角形的性质;熟练掌握三角形内角和定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
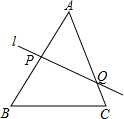 如图,直线l分别交△ABC的边AB、AC于点p、Q,若$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1.则直线1必过△ABC的( )并给予证明.(A)内心;(B)外心;(C)重心;(D)垂心.
如图,直线l分别交△ABC的边AB、AC于点p、Q,若$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1.则直线1必过△ABC的( )并给予证明.(A)内心;(B)外心;(C)重心;(D)垂心.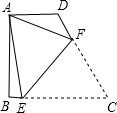 如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.
如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.
 如图,等边三角形ABC内有一点O,OA=4,OB=3,OC=5,求∠AOB的度数.
如图,等边三角形ABC内有一点O,OA=4,OB=3,OC=5,求∠AOB的度数. 如图,已知AB∥CD,∠B=76°,CM平分∠BCE,CN⊥CM,则∠DCN的度数是33°.
如图,已知AB∥CD,∠B=76°,CM平分∠BCE,CN⊥CM,则∠DCN的度数是33°.