题目内容
15.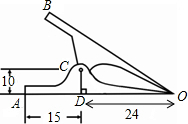 如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15mm,DO=24mm,DC=10mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.
如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15mm,DO=24mm,DC=10mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.
分析 连结AB,延长OC交AB于H,如图,Rt△OCD中,根据勾股定理计算出OC=26,再根据轴对称图形的性质得CH⊥AB,AH=BH,接着证明OCD∽△OAH,然后利用相似比计算出AH=15,从而可得AB的长.
解答  解:连结AB,延长OC交AB于H,如图,
解:连结AB,延长OC交AB于H,如图,
在Rt△OCD中,OC=$\sqrt{C{D}^{2}+O{D}^{2}}$=$\sqrt{{10}^{2}+2{4}^{2}}$=26,
∵铁夹的剖面图是轴对称图形,
∴CH⊥AB,AH=BH,
∵∠DOC=∠HOA,
∴△OCD∽△OAH,
∴$\frac{CD}{AH}$=$\frac{OC}{OA}$,即$\frac{10}{AH}$=$\frac{26}{39}$,
∴AH=15,
∴AB=2AH=30(mm).
答:A,B两点间的距离为30mm.
点评 本题考查了相似三角形的应用:利用相似三角形对应边的比相等的性质求物体的长度.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
5.小明沿着坡度为1:2的山坡向上走了1 000m,则他升高了( )
| A. | 200$\sqrt{5}$m | B. | 500m | C. | 500$\sqrt{3}$m | D. | 1000m |

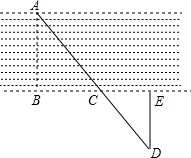 为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )
为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )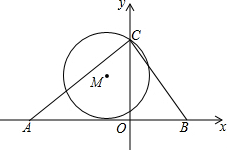 如图,在△ABC中,AB=10,AC=8,BC=6.点A、B、C都在坐标轴上.⊙M过点C且与x轴相切.设点M(x,y).
如图,在△ABC中,AB=10,AC=8,BC=6.点A、B、C都在坐标轴上.⊙M过点C且与x轴相切.设点M(x,y).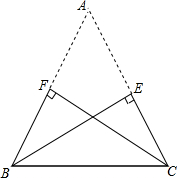 如图是缺了一个角的三角形纸片ABC,已知BE⊥AC,垂足为E,CF⊥AB,垂足为F,且BE=CF,请你根据以上条件判断△ABC的形状,并说明理由:
如图是缺了一个角的三角形纸片ABC,已知BE⊥AC,垂足为E,CF⊥AB,垂足为F,且BE=CF,请你根据以上条件判断△ABC的形状,并说明理由: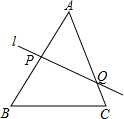 如图,直线l分别交△ABC的边AB、AC于点p、Q,若$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1.则直线1必过△ABC的( )并给予证明.(A)内心;(B)外心;(C)重心;(D)垂心.
如图,直线l分别交△ABC的边AB、AC于点p、Q,若$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1.则直线1必过△ABC的( )并给予证明.(A)内心;(B)外心;(C)重心;(D)垂心.