题目内容
9．先化简，再求值：$a（{a-b}）-2（{a-2b}）（{a+2b}）-{（{a-\frac{1}{2}b}）^2}$，其中a=-$\frac{1}{2}$，b=2．分析 先算乘法，再合并同类项，最后代入求出即可．
解答 解：$a（{a-b}）-2（{a-2b}）（{a+2b}）-{（{a-\frac{1}{2}b}）^2}$
=a2-ab-2a2+8b2-a2+ab-$\frac{1}{4}$b2
=-2a2+$\frac{31}{4}$b2，
当a=-$\frac{1}{2}$，b=2时，原式=29．
点评 本题考查了整式的混合运算和求值的应用，能运用整式的运算法则进行化简是解此题的关键，难度适中．
练习册系列答案
相关题目
19．在直角坐标系中，点P（-2，3）向右平移3个单位长度后的坐标为（ ）
| A． | （-2，6） | B． | （1，3） | C． | （1，6） | D． | （-5，3） |
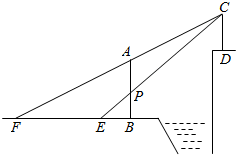如图，AB、CD是两个过江电缆的铁塔，塔AB高40米，AB的中点为P，已知：人在塔底B点以西50米的地面E点恰好看到点E、P、C在一直线上，再向西前进150米后从地面F点恰好看到点F、A、C在一直线上，求两铁塔轴线间的距离（即直线AB、CD间的距离）
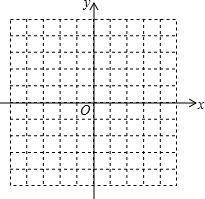已知在等腰△ABC中，AB=AC，对称轴为x轴，点A的坐标为（-3，0），点B的坐标为（1，3）．
14．在函数y=$\sqrt{2-x}$中，自变量x的取值范围是（ ）
| A． | x≥2 | B． | x≤2 | C． | x＞2 | D． | x＜2 |
1．
如图，在平行四边形ABCD中，AB=3，BC=5，对角线AC、BD相交于点O，则OA的取值范围是（ ）
如图，在平行四边形ABCD中，AB=3，BC=5，对角线AC、BD相交于点O，则OA的取值范围是（ ）| A． | 2＜OA＜5 | B． | 2＜OA＜8 | C． | 1＜OA＜4 | D． | 3＜OA＜8 |
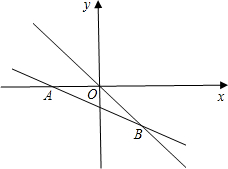如图，在平面直角坐标系中，直线y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$与x轴交于点A，与直线y=-$\frac{\sqrt{3}}{2}$x交于点B．